LeetCode-391 完美矩形

发表于 分类于 本文字数： 1.7k 阅读时长 ≈ 2 分钟

本文为LeetCode 391 完美矩形的题解。

391. 完美矩形 - 力扣（LeetCode） (leetcode-cn.com)链接

题目大意

给你一个数组 rectangles ，其中 rectangles[i] = [xi, yi, ai, bi] 表示一个坐标轴平行的矩形。这个矩形的左下顶点是 (xi, yi) ，右上顶点是 (ai, bi) 。

如果所有矩形一起精确覆盖了某个矩形区域，则返回 true ；否则，返回 false 。

示例

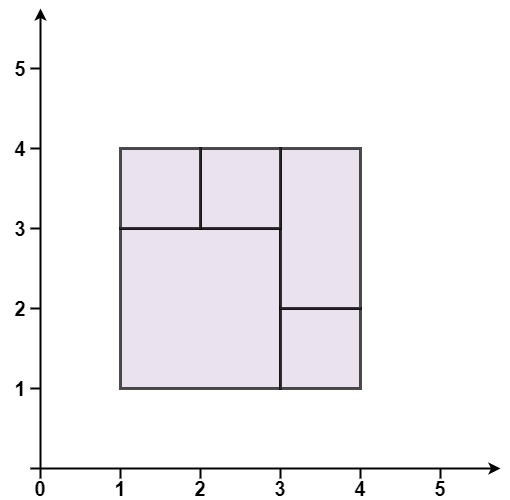
输入： rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]] 输出： true 解释： 5 个矩形一起可以精确地覆盖一个矩形区域。

解题思路

感觉与其说是算法题，还不如说是找规律…

一开始我还想对输入的矩阵进行排序，利用线段树来进行操作，后面才发现是我想多了…

考虑矩形的四个顶点，当加入一个矩形的时候，用一个map来记录顶点，如果该顶点已经被加入过，那就消除该顶点在map中的记录，否则加入map进行标记。

如果所有矩形都精准覆盖了某个矩形区域，那么肯定只会剩下最大范围矩形区域的四个顶点，我们只需要判断最后map是否只剩下4个元素，并且这四个元素分别是最大矩形区域的四个顶点就行，另外我还添加了矩形面积的判断，加强约束。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
typedef pair<int, int> Point;
#define min(a,b)  (a<b? a:b)
#define max(a,b)  (a>b? a:b)
public:
    bool isRectangleCover(vector<vector<int>>& rectangles) {
        map <Point, int> cnt;
        int minx, miny, maxx, maxy, cntS;
        minx = miny = (int)1e6;
        maxx = maxy = -(int)1e6;
        cntS = 0;
        for (const auto item : rectangles) {
             Point Point1(item[0], item[1]);
             Point Point2(item[2], item[1]);
             Point Point3(item[0], item[3]);
             Point Point4(item[2], item[3]);
             if (cnt.find(Point1) != cnt.end())  cnt.erase(Point1);   else cnt[Point1] = 1;
             if (cnt.find(Point2) != cnt.end())  cnt.erase(Point2);   else cnt[Point2] = 1;
             if (cnt.find(Point3) != cnt.end())  cnt.erase(Point3);  else cnt[Point3] = 1;
             if (cnt.find(Point4) != cnt.end())  cnt.erase(Point4);    else cnt[Point4] = 1;

             minx = min(item[0], minx);  minx = min(item[2], minx);
             maxx = max(item[0], maxx);  maxx = max(item[2], maxx);
             miny = min(item[1], miny);  miny = min(item[3], miny);
             maxy = max(item[1], maxy);  maxy = max(item[3], maxy);
             cntS += (item[3] - item[1]) * (item[2] - item[0]);
        }
        return cnt.size() == 4 && ((maxx-minx) * (maxy-miny) == cntS) 
        && cnt.count(Point(minx, miny)) && cnt.count(Point(minx, maxy)) 
        && cnt.count(Point(maxx, miny)) && cnt.count(Point(maxx, maxy));
    }
};