Games101-Lecture10-13(Geometry)学习笔记
本章内容
本文主要讲述图形学中的几何形体,包含几何的存储、渲染问题等。 几何可以分为两种不同的表示方式,分别为Implicit(隐式几何)、Explicit(显式几何)。
Implicit(隐式几何)
不直接提供点的具体坐标,而是提供点满足的关系。 E.g. 球: \[ x^2+y^2+z^2 = 1 \]

- 缺点:很难直观看出图像是什么形状,具体有哪些点在上面。
- 优点:给一个具体的点,很容易判断该点是否在表面上、表面内还是表面外,只需要带入f(x, y, z)的表达式,f(x, y, z) < 0在表面内,f(x, y, z) > 0在表面外。
Explicit(显式几何)
直接给出:三角形面,直接把一个三角形面表示出来
参数映射,给一个u、v,将其映射到三维空间,(马鞍面),(感觉有些类似曲面的参数方程形式)
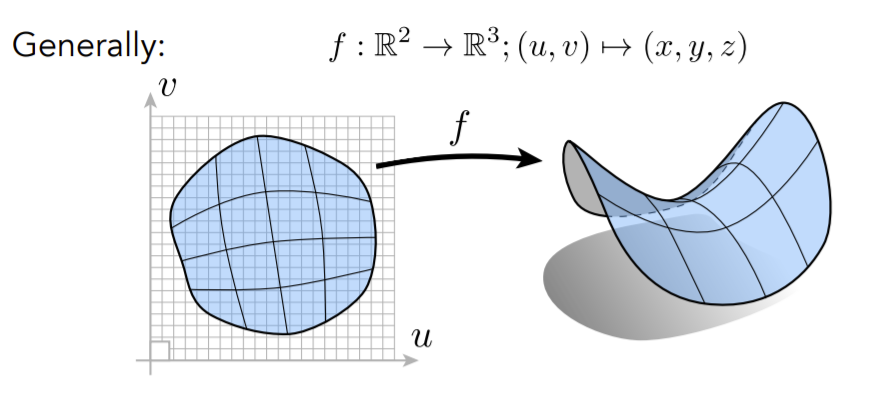
优点:显示形状很方便。
缺点:判断在表面内还是表面外比较麻烦。
隐式几何和显式几何比较
没有比较好的结合两者的方法,需要根据实际情况去选择。
更多隐式几何的例子
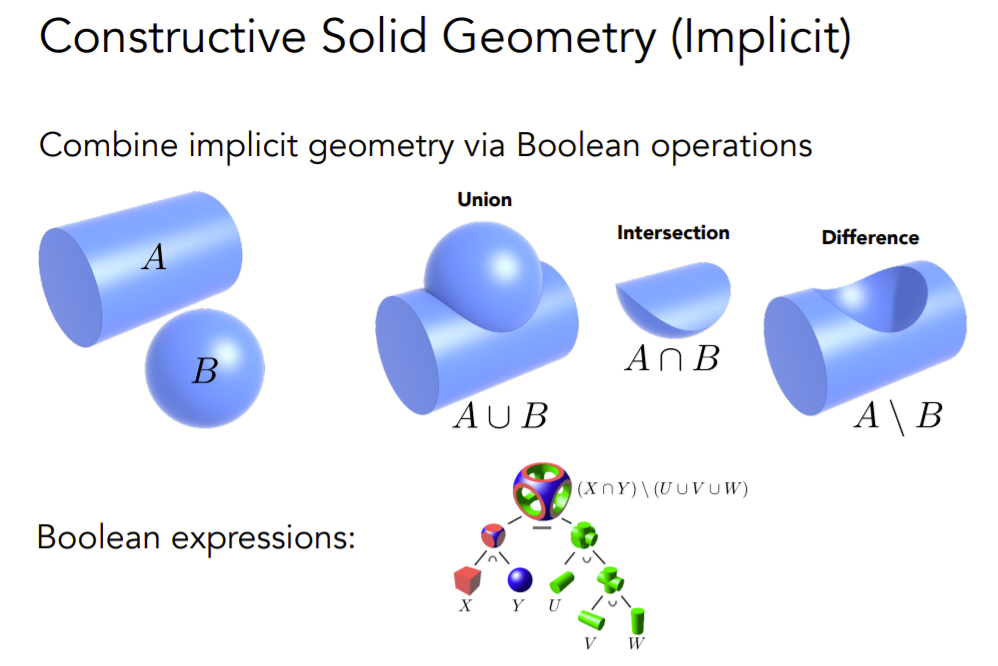
Constructive Solid Geometry(Implicit)
隐式几何不一定要通过代数式子来表示,也可以通过CSG(Constructive Solid Geometry)来表示。
CSG:对基本几何的布尔运算。
这样可以把简单的几何变成复杂的几何。
Distance Functions(Implicit)
对距离函数做一个blend
SDF
优点:
表示起来很容易。
存储有利,支持查询在物体里面还是外面。
隐式函数表达比较容易与光线求交。(之后再提)
能够严格地描述一个物体。
缺点:
- 很难描述一个复杂的物体,比如奶牛。
更多显式几何的例子
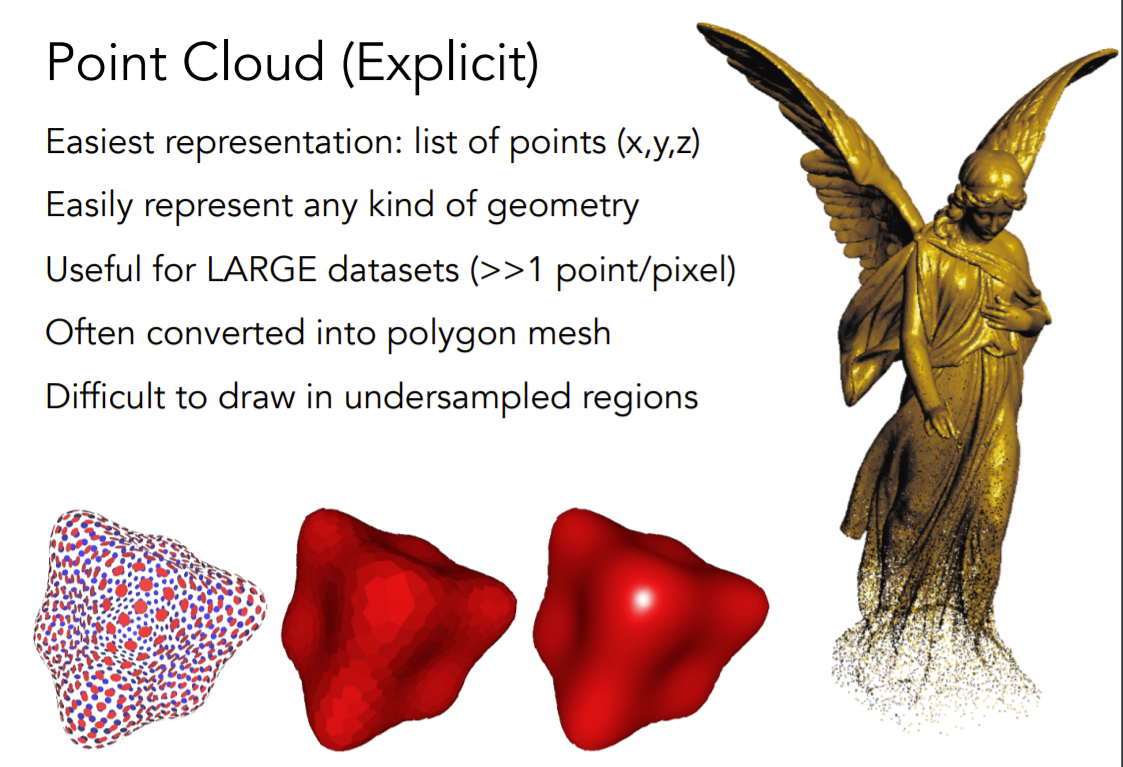
点云(Point Cloud)
我们不考虑物体的这个表面,而是考虑将物体表面上的每个点都表示出来,只要我们表示的足够细,就感受不到点与点之间的间隙。
如下图,雕像上方的点云密度比较大,下方比较稀疏,上方更容易看出物体。如果想要通过点云来表示复杂的图形,需要非常大量且密集的点云,理论上只要点云足够多足够密,就能够表示出任何物体。
Polygon Mesh(最广泛应用的显式表示)
多边形面,通过三角形、四边形来描述各种各样复杂的物体。

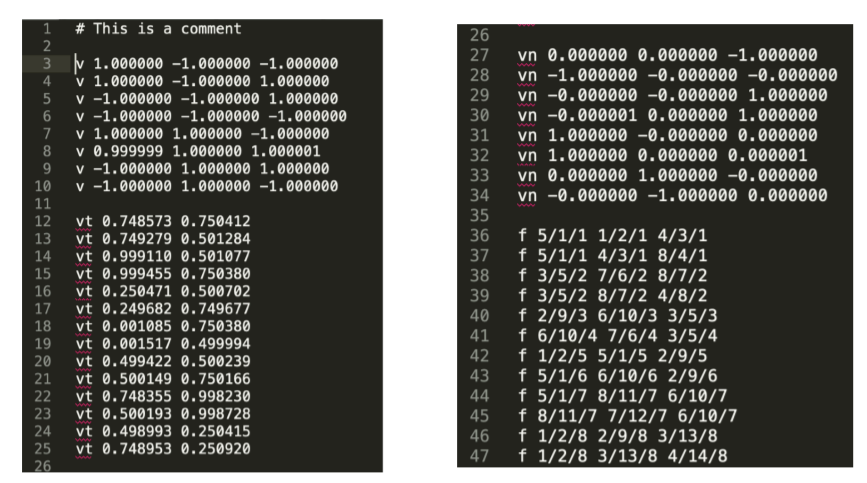
The Wavefront Object File(.obj) Format,obj文件
obj文件只是一个文本文件,指定顶点,法线,纹理坐标和它们的连接关系,依次来描述一个物体。
Curves(曲线)
本章对于曲线并不深入研究,曲线可以另外再开一堂课程专门学习,详见:https://www.bilibili.com/video/av66548502
贝塞尔曲线
光滑的曲线。
用一系列的控制点来定义某一个曲线,这些控制点会定义曲线满足的某些性质。并不要求曲线一定经过所有的控制点,但是定义曲线一定要经过起点和终点,起始位置是3(p1-p0),终点位置是3(p3-p2)。
因为是通过参数来定义的,所以是显式表示。
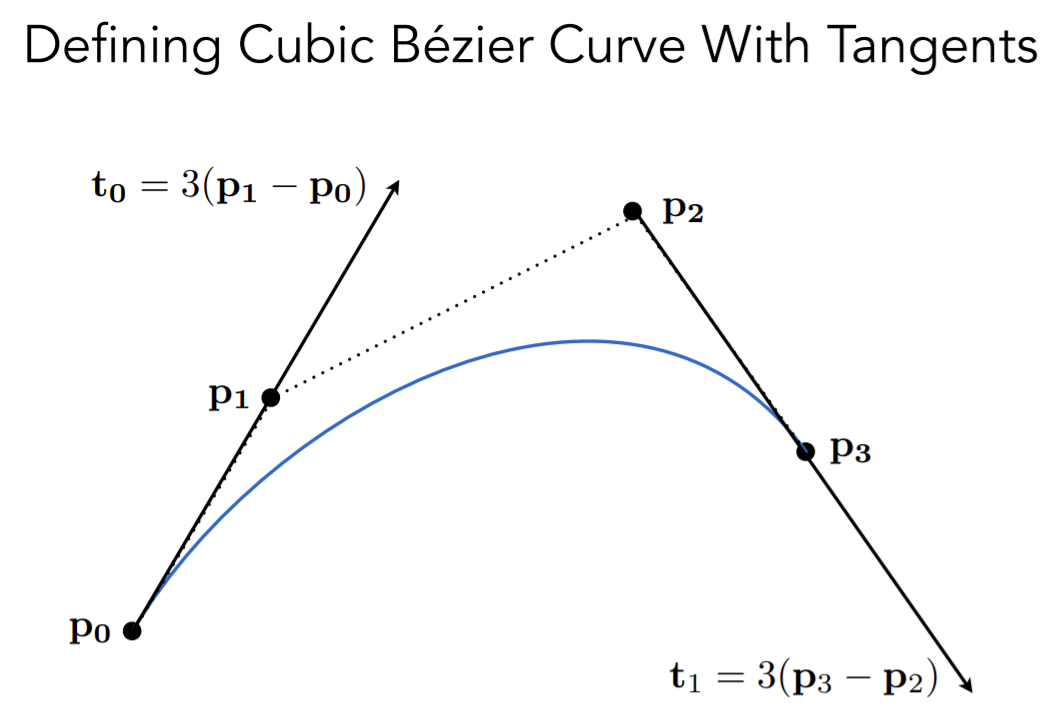
迪卡斯特里奥算法
枚举所有的时间t,通过递归的思想找到这些点,然后就能将贝塞尔曲线画出来。

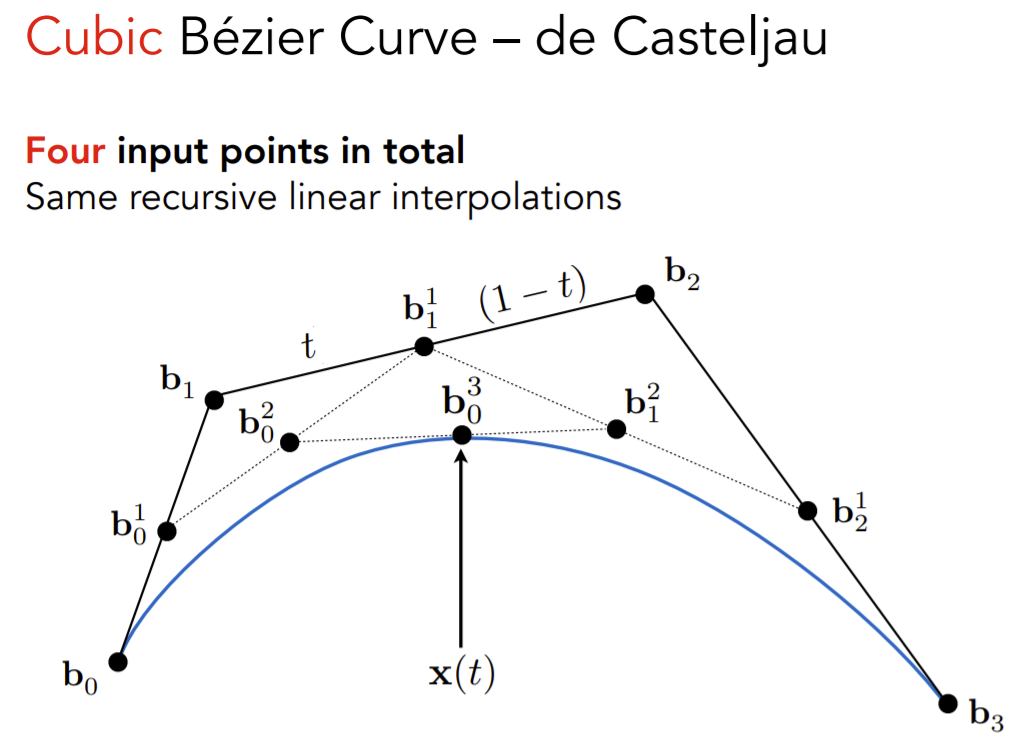
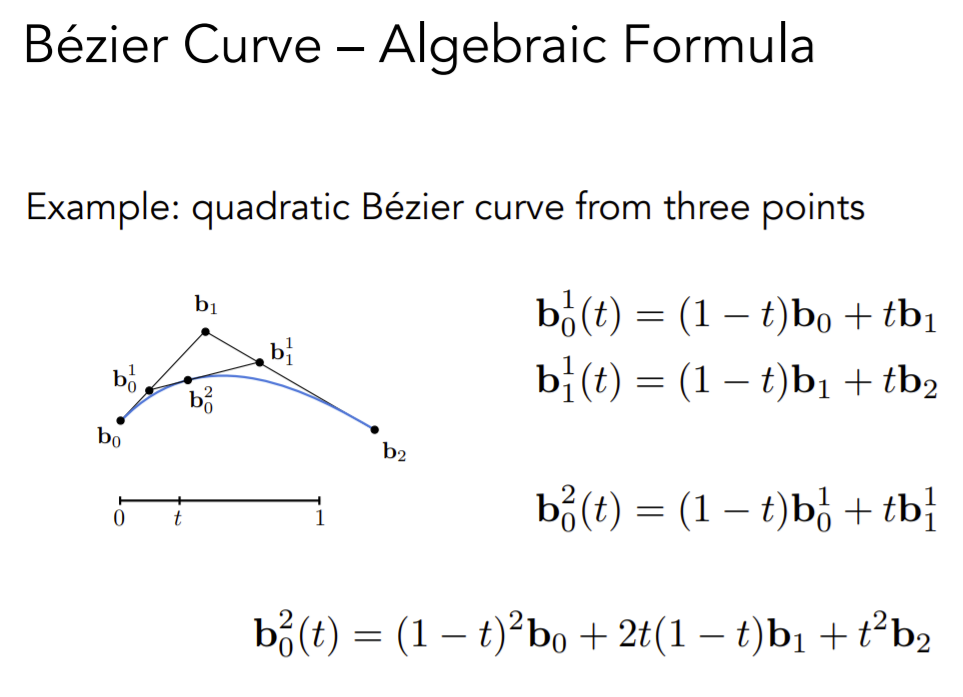
计算贝塞尔表达式
伯恩斯坦多项式,相当于对1自身的多项式展开,可以看成[t+(1-t)]^n的多项式展开。
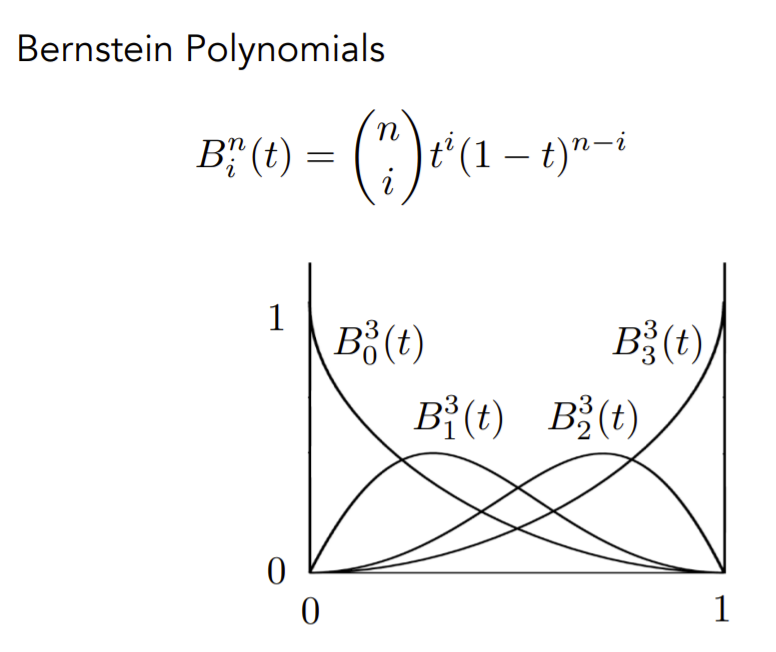
贝塞尔曲线的性质
- 并不要求曲线一定经过控制点,但是定义曲线一定要经过起点和终点。
- 起始位置是3(p1-p0),终点位置是3(p3-p2)。
- 对贝塞尔曲线的仿射变换可以用在控制点上,对控制点进行仿射变换后,再重新画出贝塞尔曲线就可以了。(仿射变换可以,但是投影不可以)
- 凸包性质:贝塞尔曲线会在控制点形成的凸包内。
- 缺点:牵一发而动全身,贝塞尔曲线如果动一个控制点,整个贝塞尔曲线都要进行变换。
逐段贝塞尔曲线
最常见的:每4个控制点定义一条贝塞尔曲线。
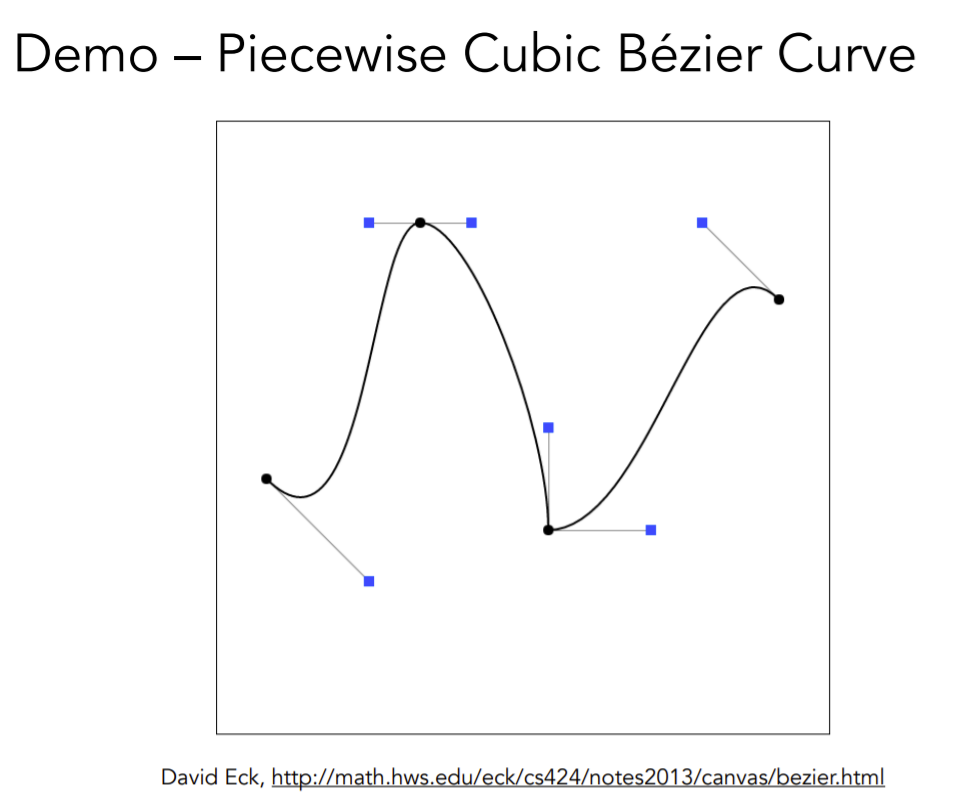
https://math.hws.edu/eck/cs424/notes2013/canvas/bezier.html
贝塞尔曲线的连续性
C1连续,即一阶导相等。
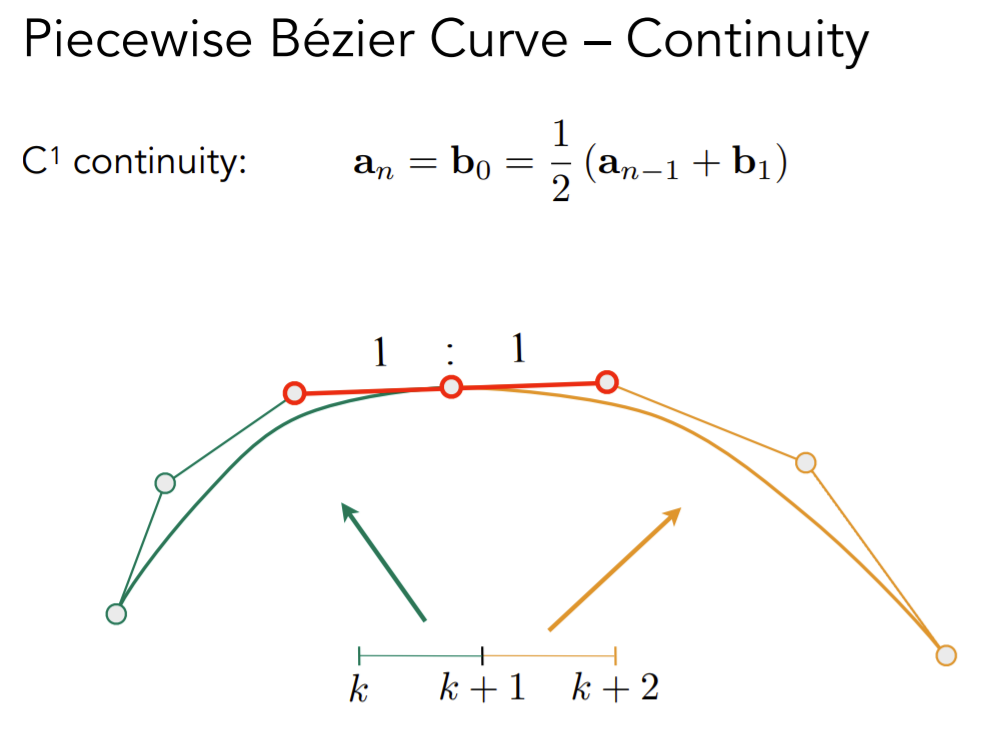
样条曲线(Splines)
- 一个连续的曲线,由一系列连续的控制点控制,在任意的敌方都能满足一定的连续性。
- 简单总结,一个可控的曲线。
B-Splines(B样条)
- 对贝塞尔曲线的一个扩展。
- 局部性:贝塞尔曲线如果动一个控制点,整个贝塞尔曲线都要进行变换,比较麻烦,B样条则不需要。
Surfaces(曲面)
贝塞尔曲面

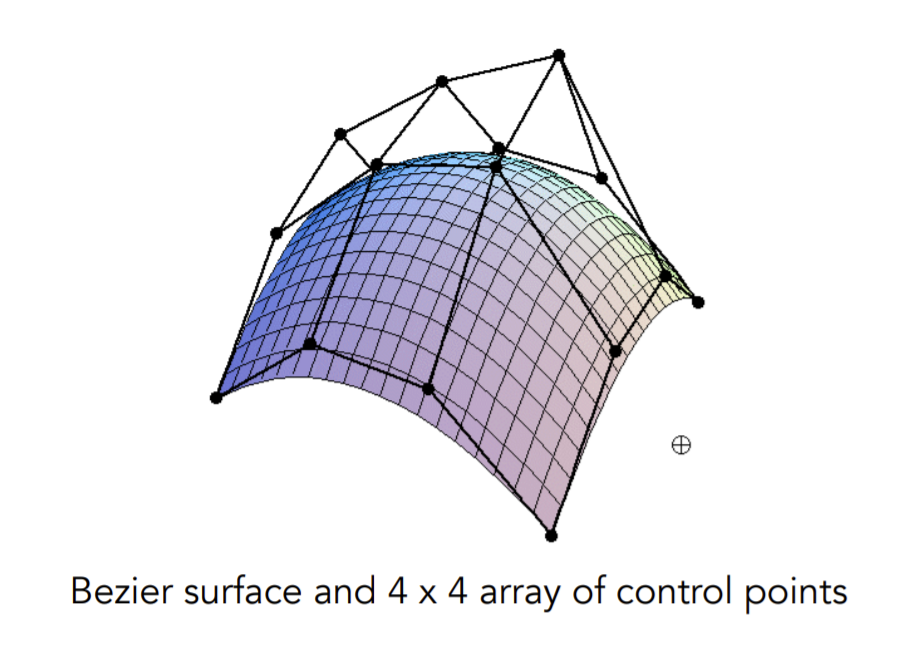
在理解了贝塞尔曲线之后,贝塞尔曲面相当于是一个从2维到3维的过渡。
如果说对于曲线来说只有一个参数0< t < 1,那么对于一个面来说,就应该有两个参数,分别设0 < u < 1, 0 < v < 1,具体过程如下图所示:
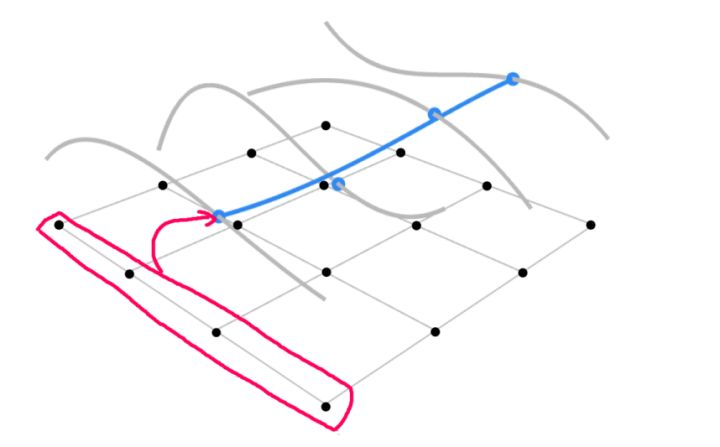
首先规定一共4x4 = 16个控制点,其水平面位置如图中16个黑点所示(并未表示出高度,防止图形太乱),将这16个点分成4列,图中红色圈中的为一列的具体例子。
在这4个控制点之下利用第一个参数 u 运用第一章的计算贝塞尔曲线的方法得到蓝色点,因为有4列,所以一共可以得到如图所示的4个蓝色点。(灰色曲线分别为每列4个点所对应的贝塞尔曲线)
在得到4个蓝色顶点之后,在这四个蓝色顶点的基础之下利用第二个参数 v 便可以成功得出贝塞尔曲面上的正确一点
遍历所有的 u,v值就可以成功得到一个贝塞尔曲面
几何处理
- 曲面细分
- 曲面简化
- 曲面规则化
曲面细分是指将一个模型的面合理的分成更多小的面,从而提升模型精度,提高渲染效果。
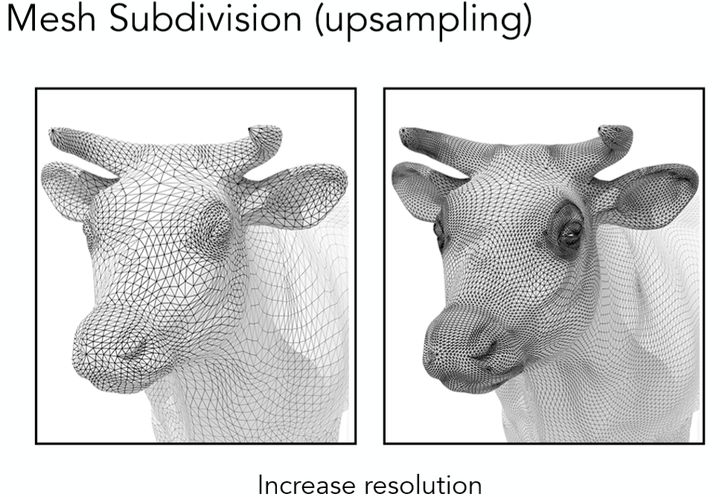
曲面简化是指将一个模型的面合理的合成更少的面,从而降低模型精度,为特定情形下提供使用(如LOD技术)

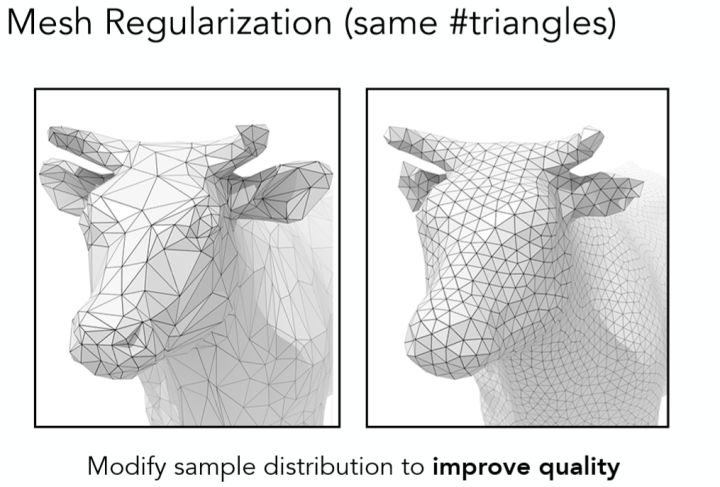
除了细分与简化之外,还有另外一种同属一类的操作叫做曲面规则化(Mesh Regularization)其所作的便是将三角面都变的尽可能相同,从而也达到提升模型效果的目的,对于该类技术本文不做详解。
曲面细分
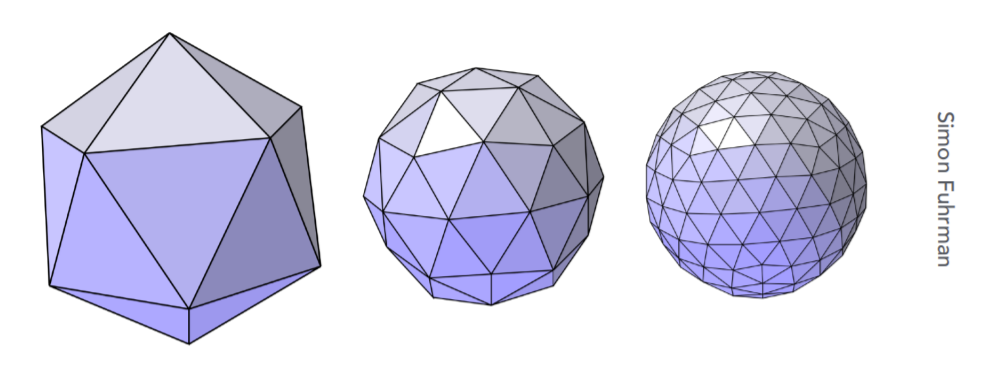
分出更多的三角形
让这些三角形的位置发生变化,使得原来的模型变得更加光滑,如下图球体:
Loop细分(Loop Subdivision)
Loop细分是一种专门针对三角形面的细分方法,步骤如下:
- 生成更多三角形或顶点
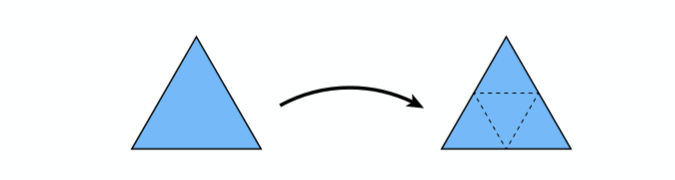
如图所示在,连接每条边的中点生成一个新的三角形,原来的三角形就会被分割成4个三角形。
- 调整这些三角形或顶点的位置
我们将所有的顶点分为两类,一类是新生成的顶点,一类是老的原来就有的顶点,对于新生成的顶点做如下处理:
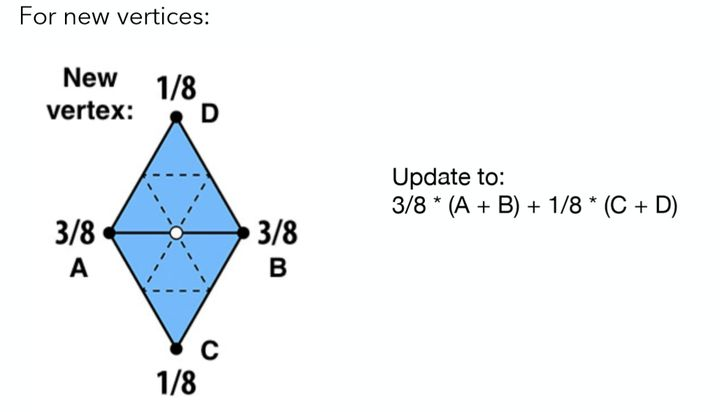
这里新的顶点就是白色的那个顶点,其位置为周围4个顶点的权重之和,各顶点权重如图所示,其余边上的新顶点处理类似。 对于旧的顶点,做如下处理:
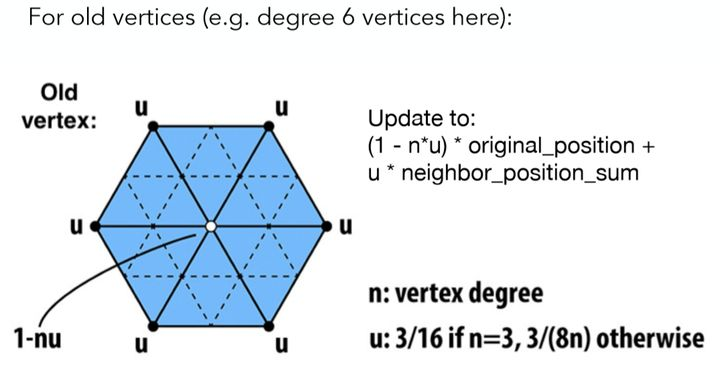
其实旧每个顶点的处理也十分类似,这里以图中一个白色旧顶点为例,也是其自身以及邻接顶点的权重和,但权重的设置与该旧顶点度数有关,具体如图中右下部分所示。 以上就是Loop细分的全过程了,最后看看效果: (这是一个不断进行Loop细分的例子)

曲面简化(Mesh Smplication)
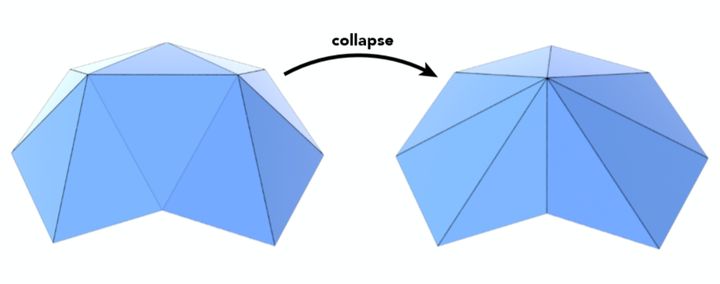
其实曲面简化所利用的一个方法叫做边坍缩,如上图所示就是将一条边的两个顶点合成为一个顶点。但随之而来的问题就是,曲面简化需要尽量保持原本模型的shape,如何坍缩一条边,或者说坍缩哪一条边能够使得原模型样貌被改变的程度最小,这就是曲面简化的关键所在。 为此引入一个度量,即二次误差度量(Quadric Error Metrics)
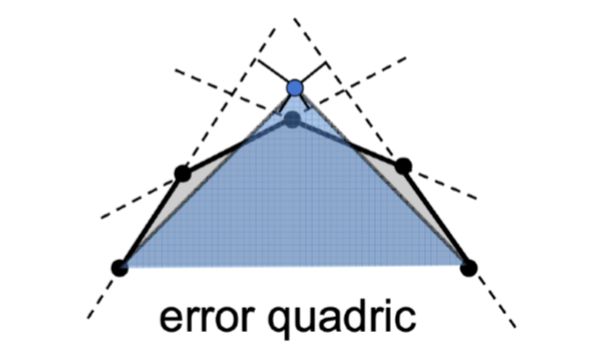
即坍缩之后蓝色新顶点所在的位置与原来各个平面的距离之和。如果能够使得这个误差最小那么对整个模型样貌修改一定程度上也会较小。 那么其实到这整个曲面简化的算法流程已经比较清晰了,可以使用堆来进行计算。
为模型每条边赋值,其值为简化这条边之后,代替两个老顶点的新顶点所能得到的最小二次误差度量
选取权值最小的边做简化,新顶点位置为原来计算得出使得二次误差最小的位置
简化完之后,与之相连其他的边的位置会改动,更新这些边的权值
重复上述步骤,直到到达终止条件
这其实是一个标准的贪心算法,可能到不了全局最优解,但事实证明最终的结果依然相当不错。
