Games101-Lecture3-4（Transformation）学习笔记
本章内容
- 变换
- 为什么要学习“变换”
- 2D变换：旋转、缩放、切变
- 齐次坐标
- 3D变换
- MVP变换（模型、视图、投影变换）
前情提要
向量 基本运算：加法、乘法。
点乘 通过点乘结果的正负用来判断前后关系。
叉乘 通过叉乘结果的朝向，可以用来判断左右关系，比如判断点是否在图形内。
矩阵计算
本章节将开启Transformation（变换）的内容，以上是变换内容的基础。
为什么要变换
在动画制作和展示中，不可避免的要涉及到视角、各种模型的变换，还有将3维空间视图转化为2维空间的变换。
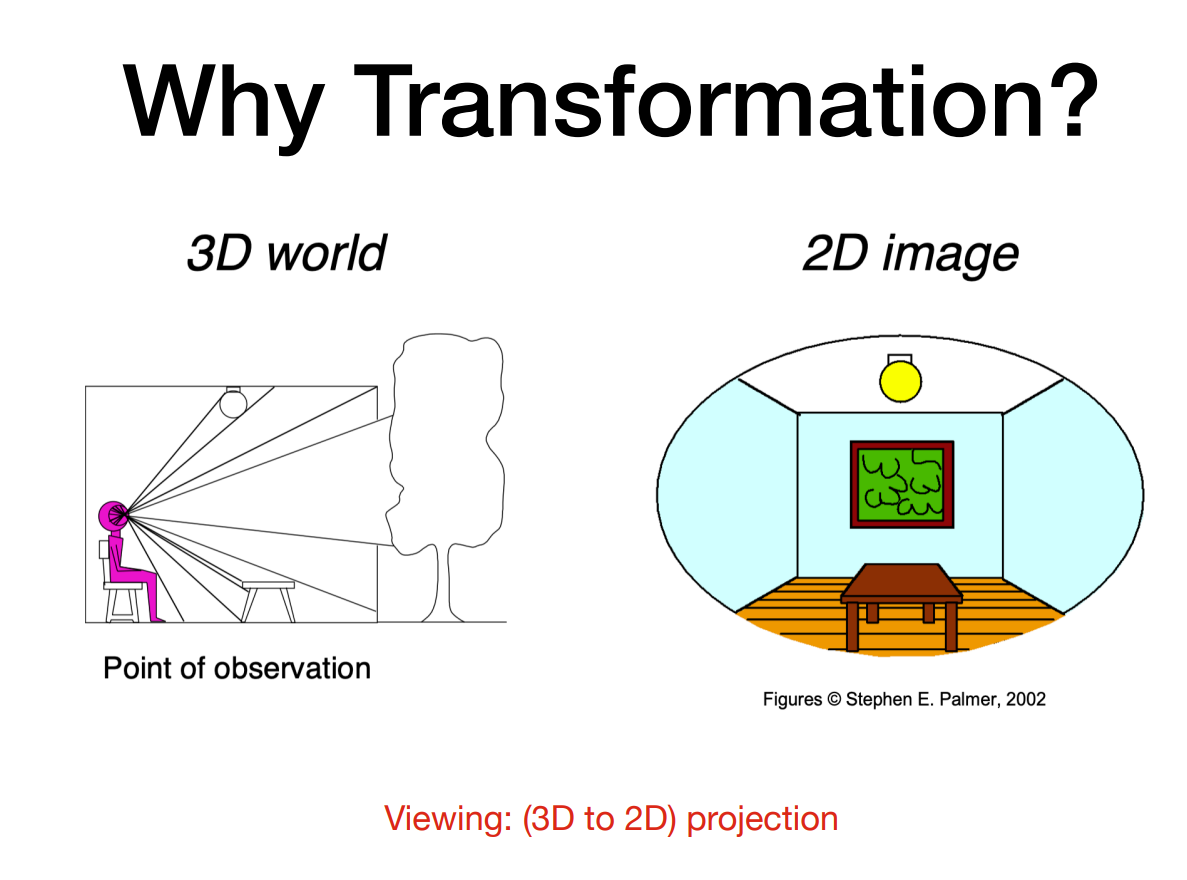
2D变换
将变换与矩阵联系起来
旋转、缩放、切变
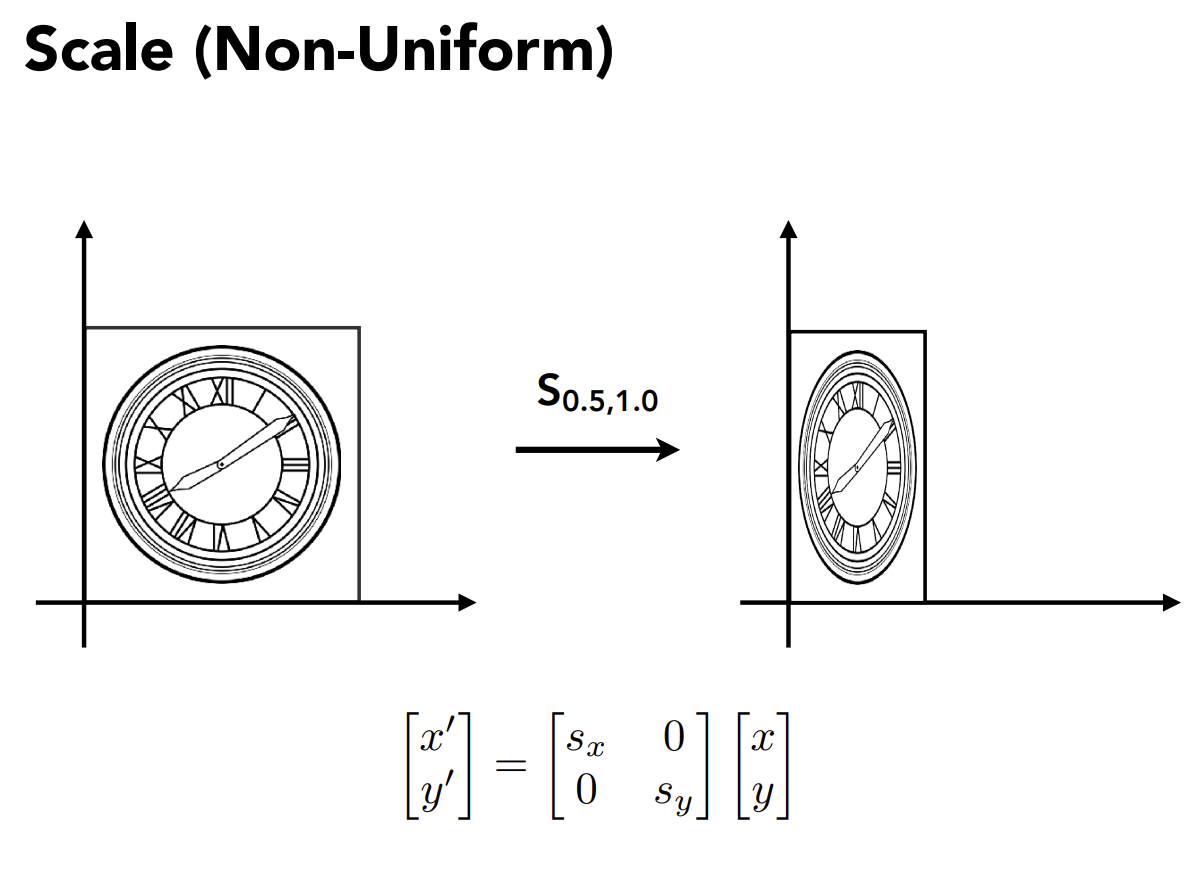
缩放
对于原来的x，y坐标，我们对于x缩小至0.5倍，y不变的一个不均匀缩放，使其左乘缩放矩阵即可。
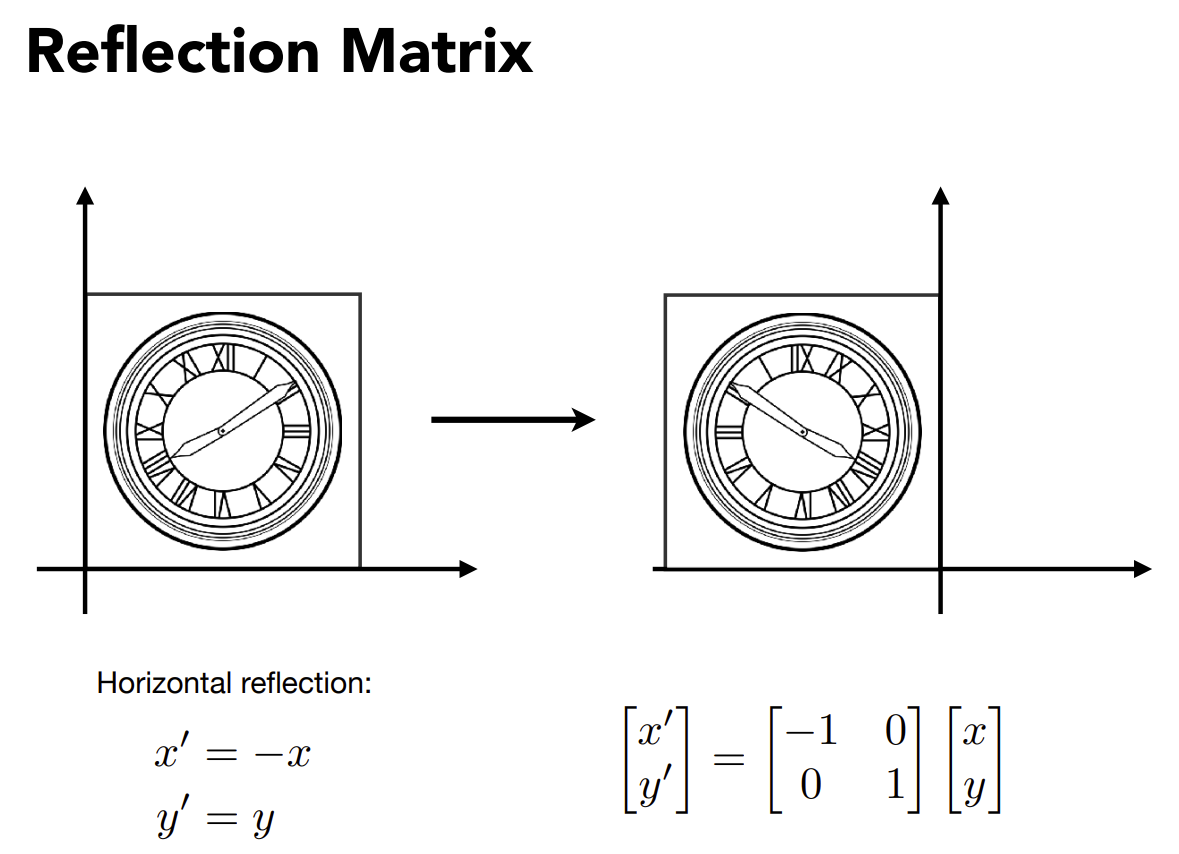
镜像
对图像以y轴做镜像变换，使其x坐标相反即可。
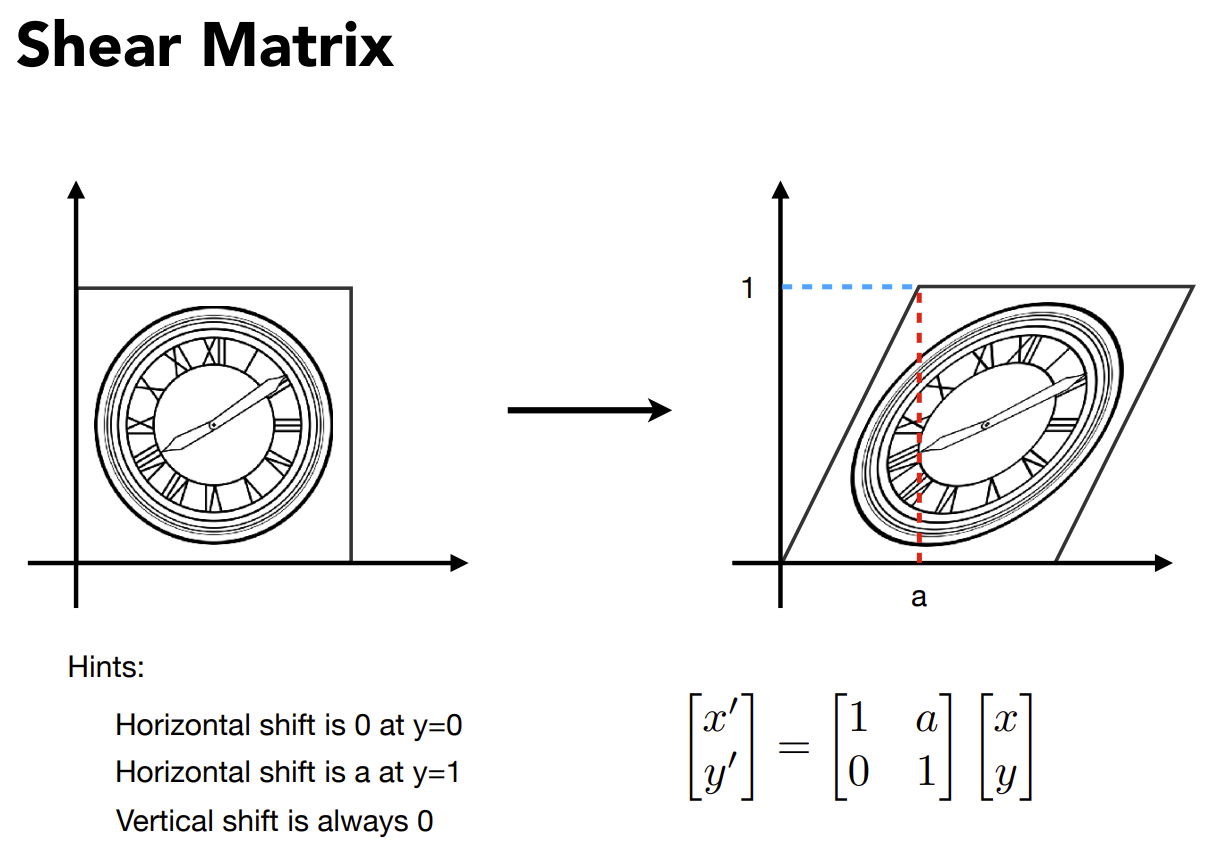
切变
y轴坐标不变，x轴移动a方向距离，如果图像y轴坐标为1，切变变换的矩阵如下。
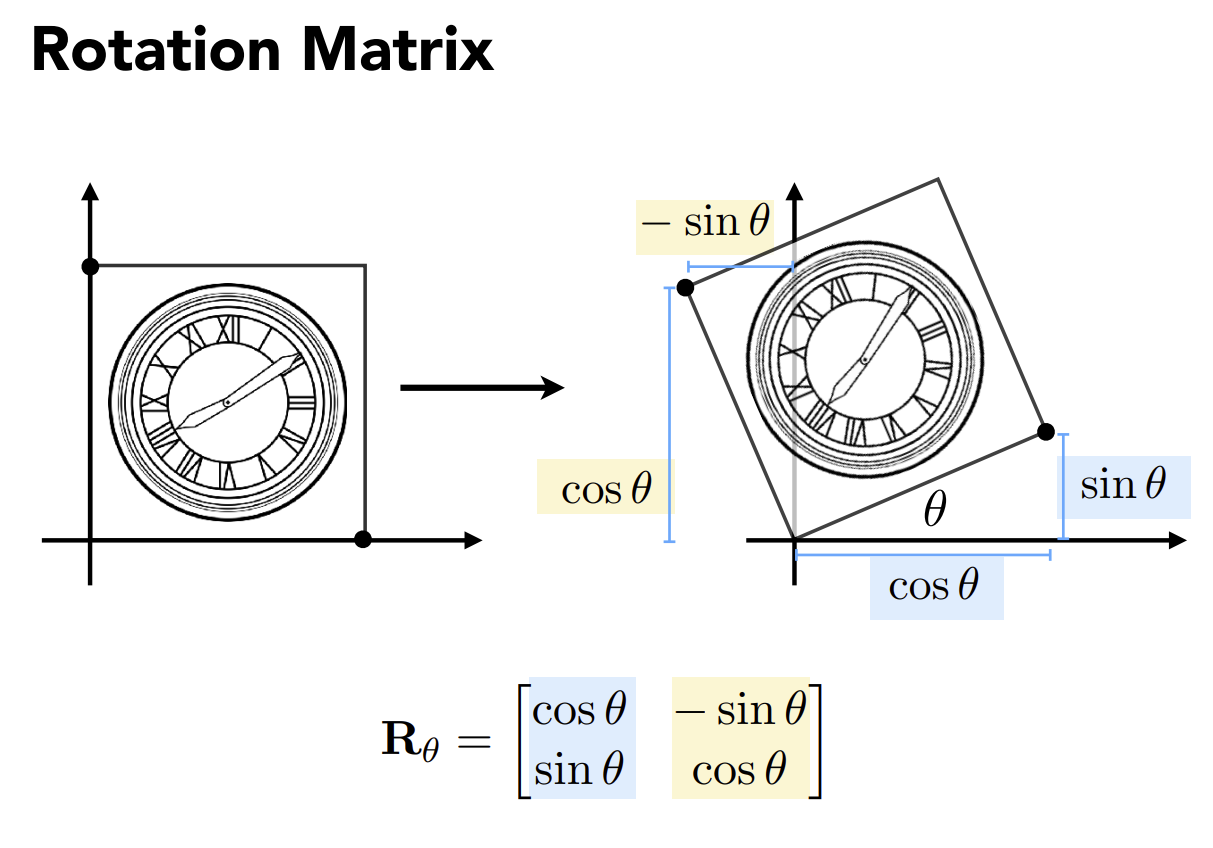
旋转
一般情况下，我们默认旋转是围绕原点逆时针旋转θ角度。对于下图的旋转，我们可以考虑2个特殊的点，即原四边形右下和左上的2个点。 假设正方形长为1，两点坐标分别为(1, 0)、(0, 1)，在旋转θ角后，两点坐标变换为(cos θ, sin θ)、(-sin θ, cos θ)，由此可以联立方程解得如下。 \[ \begin{bmatrix} cos\theta \\ sin\theta \\ \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ \end{bmatrix} \]
\[ \begin{bmatrix} -sin\theta \\ cos\theta \\ \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix} \begin{bmatrix} 0 \\ 1 \\ \end{bmatrix} \]
线性变换（矩阵）
以上的变换都可以转换成如下的线性变换，通过矩阵乘法改变坐标。 \[ \begin{bmatrix} x' \\ y' \\ \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ \end{bmatrix} \]
\[ \begin{split} x' = ax + by \\ y' = cx + dy \\ x' = M x \end{split} \]
齐次坐标
为什么引入齐次坐标
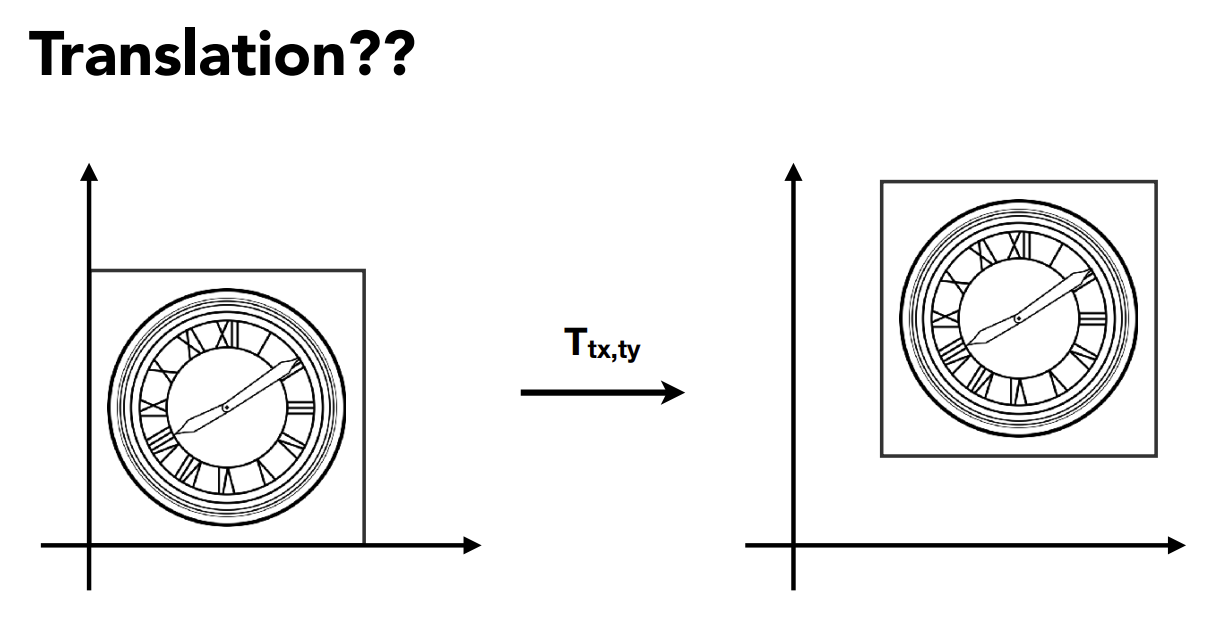
因为平移变换比较特殊，对于如上的坐标平移，我们虽然能够直接写出 \[ \begin{split} x' = x + t_x \\ y' = y + t_y \\ \end{split} \] 但是，我们无法将其写成如上的二维矩阵乘法形式，我们只能写成如下形式，因此平移操作并不属于我们如上定义的线性变换。 我们考虑如何将平移变换加入线性变换，能将各种变换统一起来，因此，我们引入齐次坐标的概念。 \[ \begin{bmatrix} x' \\ y' \\ \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \\ \end{bmatrix} \]
仿射变换（线性变换 + 平移）
对于n的维度，我们可以在表示的时候增加一个维度。
\[ 2维点 = (x, y, 1)^T \]
\[ 2维向量 = (x, y, 0)^T \]
\[ \begin{pmatrix} x \\ y \\ w \\ \end{pmatrix} = \begin{pmatrix} x/w \\ y/w \\ 1 \\ \end{pmatrix} , (w \neq 0) \]
因此可以得到如下（2维坐标）
- 向量 + 向量= 向量
- 点 - 点 = 向量
- 点 + 向量 = 点
- 点 + 点 = 两点的中点
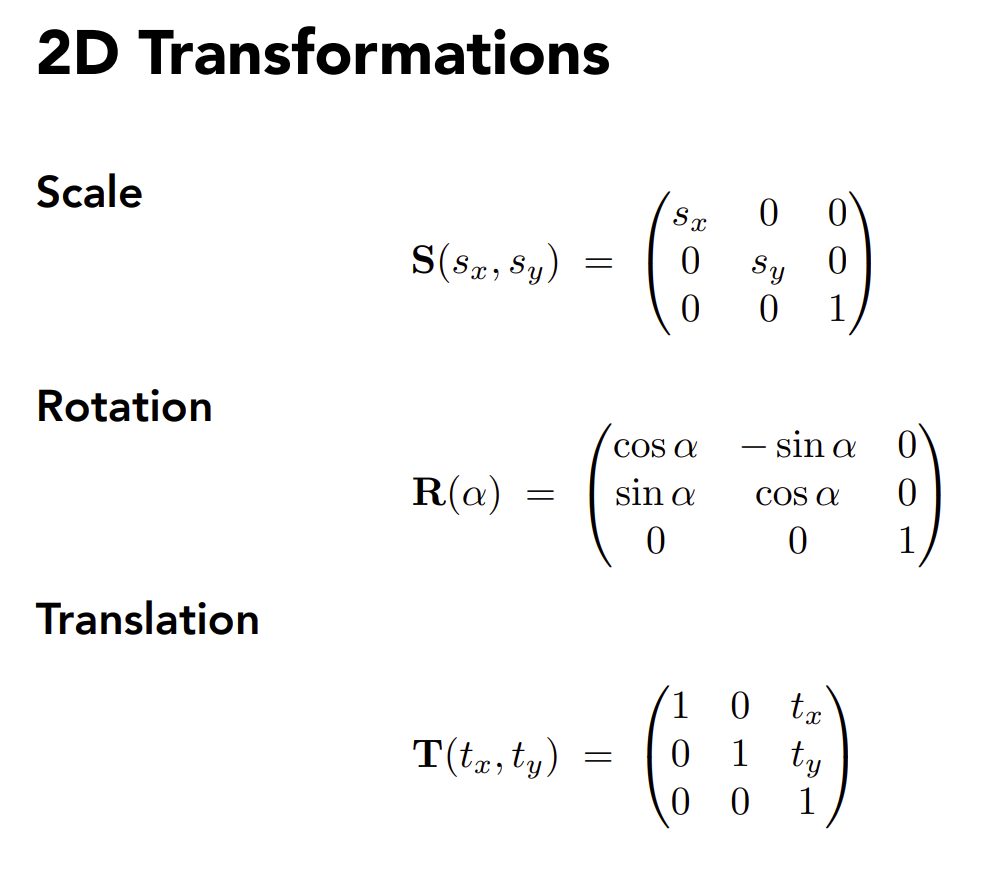
因此在2维空间下，线性变换可以表示如下：
分解放射变换
仿射变换顺序
- 矩阵乘法不满足交换律，不能随意改变乘法的顺序。
- 同时因为是左乘变换矩阵，我们可以先将左边的变换矩阵结合起来，将左边变成一个变换矩阵。
\[ A_n(...A_2(A_1(x))) = A_n···A_2·A_1· \begin{pmatrix} x \\ y \\ 1 \\ \end{pmatrix} \]
- 同时，仿射变换是先线性变换，再平移变换。
绕非原点旋转
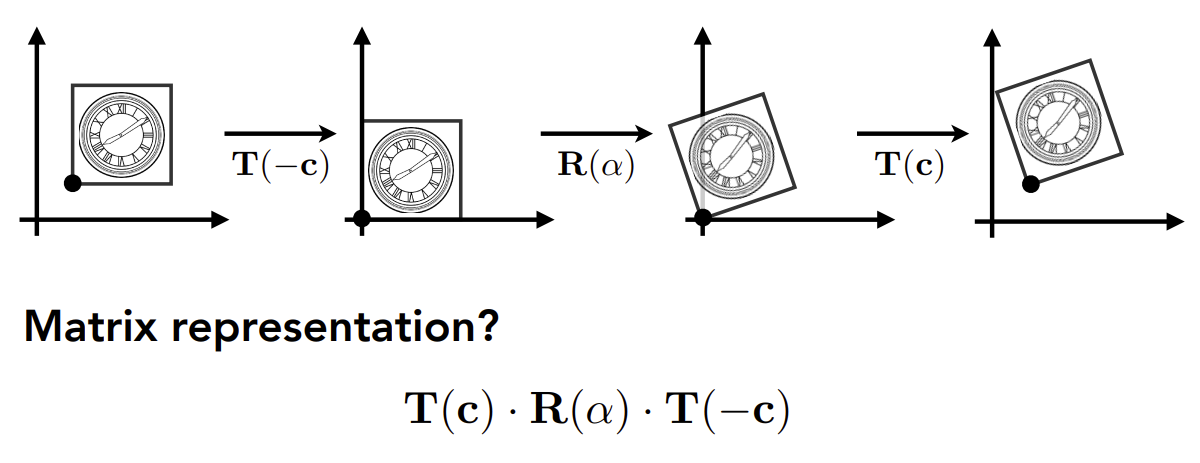
由于旋转默认是以原点为中心的，因此如果我们想绕非原点进行旋转，可以拆分成以下3步：
- 将旋转中心平移至原点，物体也进行相同的平移变换。
- 物体绕原点旋转。
- 物体平移回去。
旋转的逆矩阵
绕原点逆时针旋转θ角度，可以理解为顺时针旋转-θ角度，可以得到以下推导，旋转矩阵是正交矩阵。 \[ R_{-\theta} = \begin{pmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta\\ \end{pmatrix} = R^T_\theta \]
\[ R_{-\theta} = R^{T}_{\theta} = R^{-1}_{\theta} \]
3D变换
缩放和平移
顺序仍然是先线性变换，再平移。
旋转
先从简单的例子开始，以绕x轴旋转为例，旋转过程中x轴的坐标保持不变，可以看作yOz平面上的旋转。 但同时也有细微区别，比如在绕y轴旋转的时候，\(\alpha\)要改成\(-\alpha\)，因为我们可以xyz坐标系后面补全，xyzxyzxyz...一直保持xyz的顺序循环下去，因此是\(\begin{cases}xy=z\\yz=x\\zx=y\end{cases}\)，绕着y轴正方向逆时针旋转的时候，此时\(xz=-y\)，所以相当于为了满足坐标系的规则，我们代入2D旋转的角度值是\(-\alpha\)
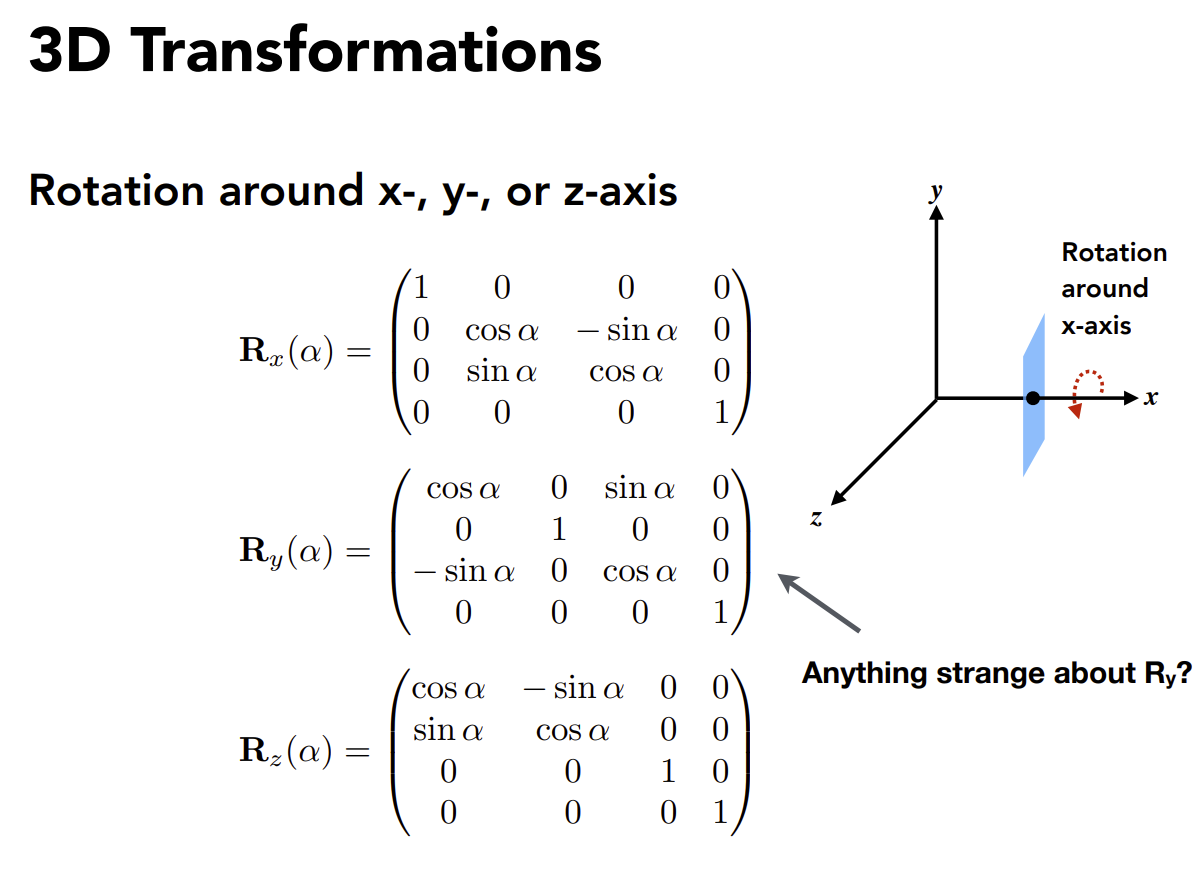
罗德里格斯旋转公式
定义绕x轴y轴z轴分别旋转α、β、γ的角度。 \[ R_{xyz}(\alpha, \beta, \gamma) = R_x(\alpha,)R_y(\beta)R_z(\gamma) \]
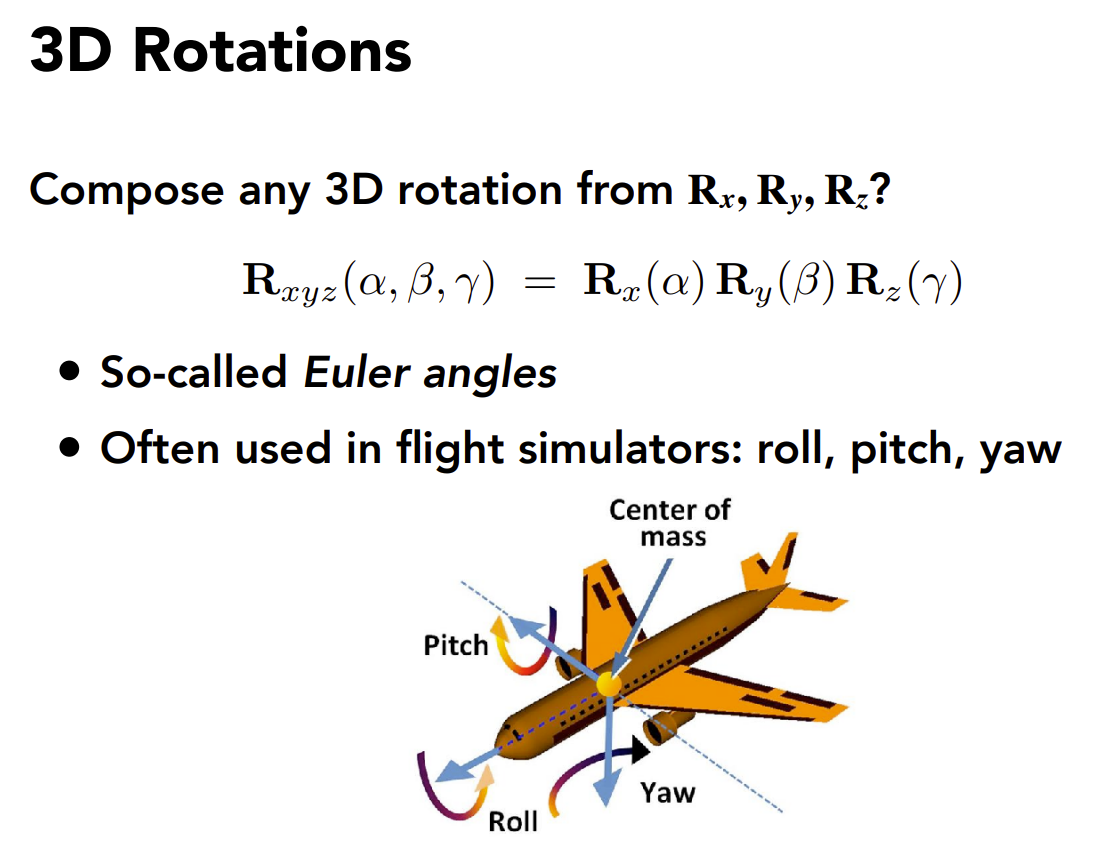
罗德里格旋转公式是计算三维空间中，一个向量绕旋转轴旋转给定角度以后得到的新向量的计算公式。这个公式使用原向量，旋转轴及它们叉积作为标架表示出旋转以后的向量。可以改写为矩阵形式，被广泛应用于空间解析几何和计算机图形学领域，成为刚体运动的基本计算公式。\(n\)表示旋转轴，\(I\)表示单位矩阵。 \[ \boldsymbol{R}(\boldsymbol{n},\alpha) = cos(\alpha)\boldsymbol{I} + (1-cos(\alpha))\boldsymbol{nn}^T + sin(\alpha) \begin{pmatrix} 0 & -n_z & n_y \\ n_z & 0 & -n_x \\ -n_y & n_x & 0 \\ \end{pmatrix} \]
视图变换（View/Camera Transformation）
视角or相机变换
定义相机
- 相机的位置
- 相机朝向的方向
- 相机上方的方向
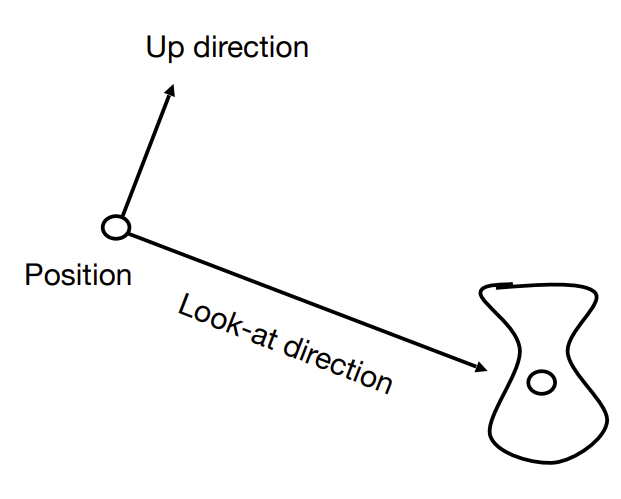
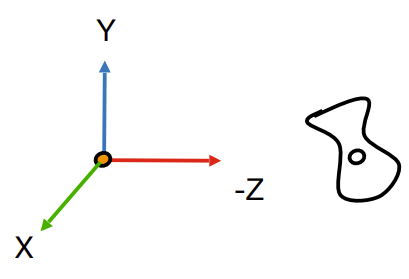
为了方便计算，我们可以将相机放在原点，相机朝向z轴的负方向，相机上方的方向是y轴正方向。同时，我们在移动相机或者视角的时候，当作相机位置和朝向始终不动，而是物体在移动。
通过\(M_{view}\)变换将相机放到标准位置上
基本思想：
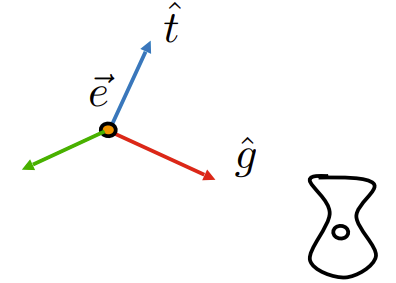
- 将\(\vec{e}\)（相机中心点）移动到原点
- 将\(\vec{g}\)旋转到z轴的负方向
- 将\(\vec{t}\)旋转到y轴的正方向
- 此时\((\vec{g} * \vec{t})\)和x轴的正方向一样
\[
\begin{align*}
M_{view} & = R_{view}*T_{view} \\
T_{view} &=
\begin{bmatrix}
1 & 0 & 0 & -x_{\vec{e}} \\
0 & 1 & 0 & -y_{\vec{e}} \\
0 & 0 & 1 & -z_{\vec{e}} \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\end{align*}
\] 以上的步骤虽然明确，但是我们很难写出这样的\(R_{view}\)矩阵来表示从\(\vec{g}\)、\(\vec{t}\)等轴旋转到z轴负方向和y轴正方向的操作。
因此我们考虑反过来表示，我们将z轴负方向和y轴正方向旋转到\(\vec{g}\)、\(\vec{t}\)等轴，再利用之前旋转的变换矩阵是正交矩阵，\(R_{-\theta} = R^{T}_{\theta} =
R^{-1}_{\theta}\)，从而可以求出\(R_{view}\)，于是我们考虑将x轴旋转到\((\vec{g} * \vec{t})\)，y轴旋转到\(\vec{t}\)，z轴旋转到\(-\vec{g}\)，同时为了保证相对运动不变，其它所有物体都需要跟着做这个变换。
\[
\begin{align*}
R^{-1}_{view} & =
\begin{bmatrix}
x_{\vec{g}*\vec{t}} & x_{\vec{t}} & x_{-\vec{g}} & 0 \\
y_{\vec{g}*\vec{t}} & y_{\vec{t}} & y_{-\vec{g}} & 0 \\
z_{\vec{g}*\vec{t}} & z_{\vec{t}} & z_{-\vec{g}} & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix} \\
\Rightarrow
R_{view} & =
\begin{bmatrix}
x_{\vec{g}*\vec{t}} & y_{\vec{g}*\vec{t}} & z_{\vec{g}*\vec{t}}
& 0 \\
x_{\vec{t}} & y_{\vec{t}} & z_{\vec{t}} & 0 \\
x_{-\vec{g}} & y_{-\vec{g}} & z_{-\vec{g}} & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix} \\
\end{align*}
\]
总结
- 物体要与相机一同移动
- 保证相机在原点，up为y轴正方向，朝向z轴负方向
投影变换
正交投影
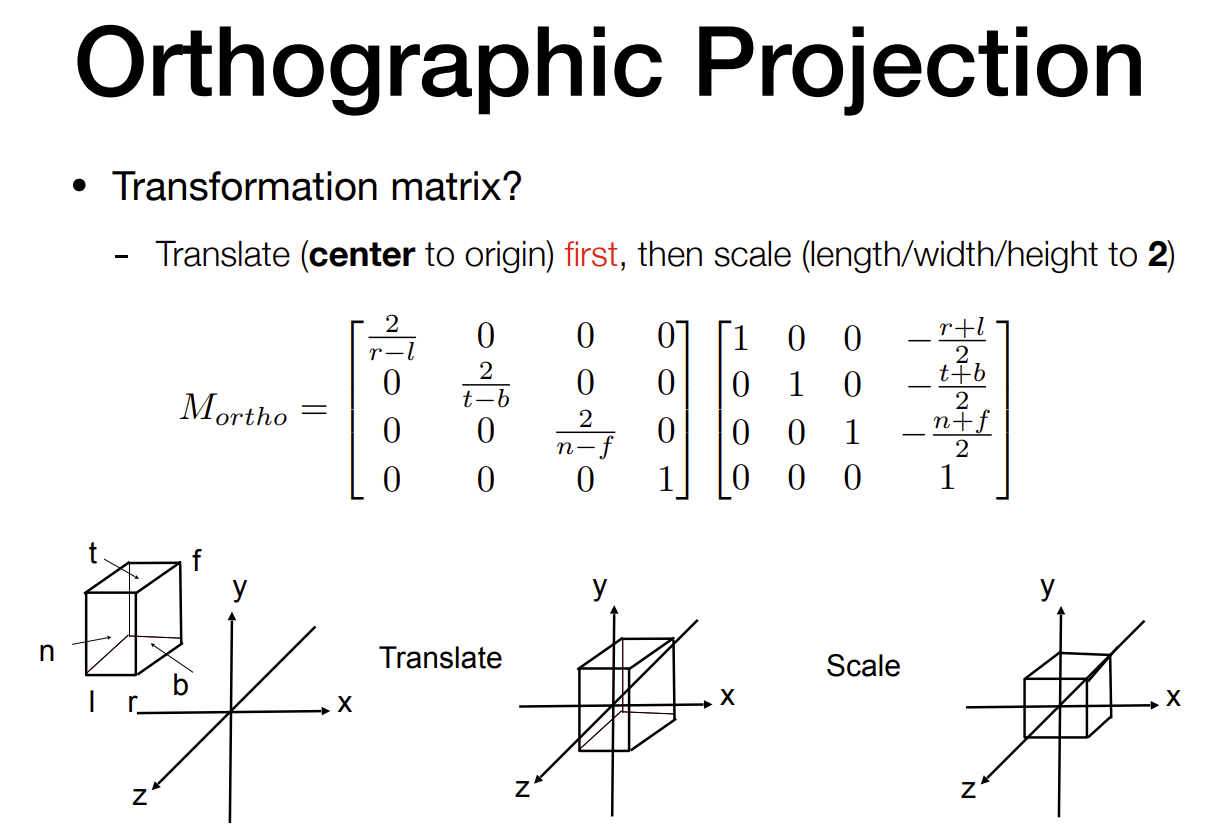
正交投影是将相机放在无限远的位置上，打出来的是平行光，相同的物体不论距离，呈现的大小一样。 如下图所示，左下角是该物体原本的位置和形状，我们需要通过正交投影使其落在\([-1, 1]^2\)里面，首先先将物体的中心移动到原点，平移矩阵为\(\begin{bmatrix}1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\)，缩放矩阵为\(\begin{bmatrix}\frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}\)
注意：之前我理解这个变换的一个误区，我一直以为缩放变换必须是等比例缩放，但实际上x轴和y轴坐标变换的比例不一定相同，只是通过缩放使其落在\([-1, 1]^2\)的区间里面，所以物体一定会被拉伸（长宽比会变换），并且在之后的视口变换会再一次被拉伸。
透视投影
特点
- 近大远小
- 原本的平行线不再平行，而是会相交于一点
- 更符合人眼观察到的图像规律
步骤
- 先从截头锥体变成长方体(\(M_{persp->ortho}\))，感性上理解有些像是将远平面f挤压到与近平面n一样大。
- 再做正交投影(\(M_{ortho}\))
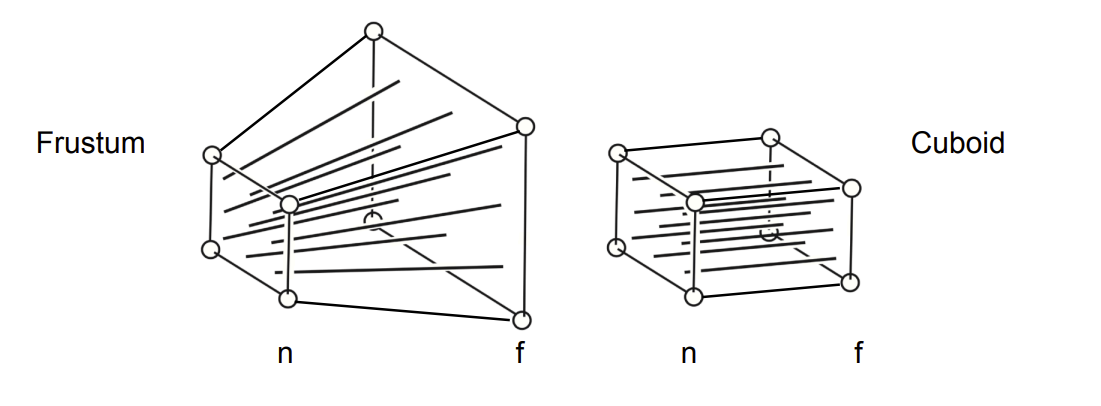
如何求得\(M_{persp->ortho}\)矩阵
远平面坐标是z，近平面坐标是n（注意这里n和f可以为负，并且大多数情况是负数，因为相机朝向z轴负方向），首先假设点远平面坐标是(x, y, z)，变换后的近平面坐标是(x', y', z')，可以根据相似三角形的比例关系得到如下比例关系和矩阵变换（由齐次坐标系的特点，x、y、z、w同乘以z，还是表示同样的点）：
\[
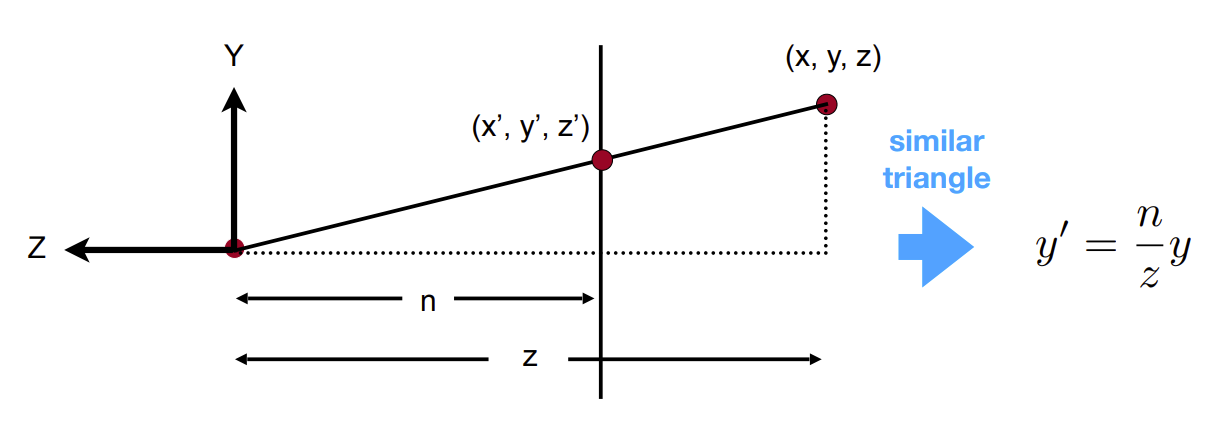\begin{cases}
y'=\frac{n}{z}y \\
x' = \frac{n}{z} x
\end{cases}
\]
\[ \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} \Rightarrow \begin{bmatrix} nx/z \\ ny/z \\ unknown \\ 1 \end{bmatrix} == \begin{bmatrix} nx \\ ny \\ unknown \\ z \end{bmatrix} \]
为了使\(M_{persp->ortho}^{(4*4)}\)矩阵对于任意的x, y都满足该变换，可得\(M_{persp->ortho}^{(4*4)}\)的第1、2、4行如下： \[ M_{persp->ortho}^{(4*4)} = \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} \] 为了求第\(M_{persp->ortho}^{(4*4)}\)的第3行，我们可以观察这个通过\(M_{persp->ortho}\)的变换，有以下特点：
- 近平面上的点的坐标不会改变
- 远平面上的点的z轴坐标不会改变
- 中间平面的点的z轴坐标会改变
将近平面上的点的坐标带入，即\(z=n\)，可得\(\begin{bmatrix} x \\ y \\ n \\ 1\end{bmatrix} \Rightarrow \begin{bmatrix} x \\ y \\ n \\ 1\end{bmatrix} == \begin{bmatrix} nx \\ ny \\ n^2 \\ n\end{bmatrix}\) 因此\(M_{persp->ortho}^{(4*4)}\)第3行必定为\(\begin{bmatrix}0 & 0 & A & B\end{bmatrix}\)的形式，因为对近平面上的任一点均满足上述等式，\(\begin{bmatrix}0 & 0 & A & B\end{bmatrix}\begin{bmatrix} x \\ y \\ n \\ 1\end{bmatrix} = n^2\)
将远平面上的点的坐标带入，即\(z=f\)，可得\(\begin{bmatrix} 0 \\ 0 \\ f \\ 1\end{bmatrix} \Rightarrow \begin{bmatrix} 0 \\ 0 \\ f \\ 1\end{bmatrix} == \begin{bmatrix} 0 \\ 0 \\ f^2 \\ f\end{bmatrix}\)，再带入可得\(\begin{bmatrix}0 & 0 & A & B\end{bmatrix}\begin{bmatrix} 0 \\ 0 \\ f \\ 1\end{bmatrix} = f^2\)
由以上两次带入可得 \[ \begin{cases} An+B=n^2 \\ Af+ B=f^2 \end{cases} \] 解得 \[ \begin{cases} A=n+f \\ B=-nf \end{cases} \] 因此 \[ M_{persp->ortho}^{(4*4)} = \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} \] 透视投影的矩阵变换为\(M_{persp} = M_{ortho} * M_{persp->ortho}\)
透视投影近平面常用到的数据
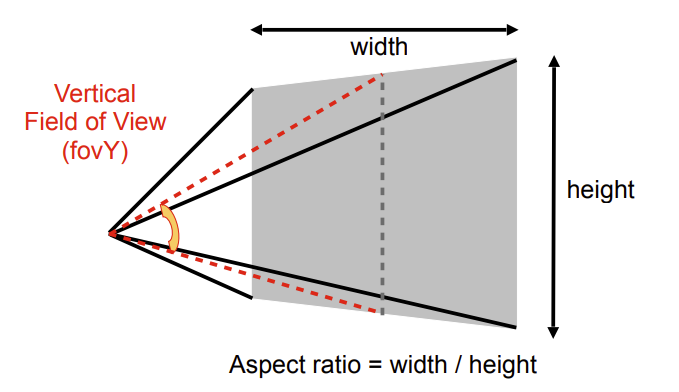
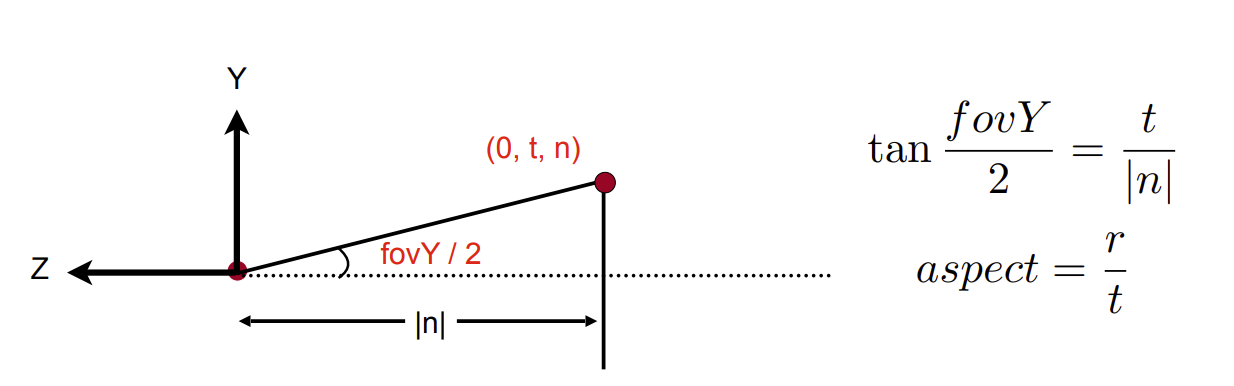
对于近平面，我们知道它与原点距离为\(|n|\)，其余分别为\(l,r,b,t\)(left, right, bottom, top)，通过以下数据可以求得。
- 垂直可视角\(fov Y\)（从相机位置向平面上边和下边分别作垂线，两条垂线的夹角）
- 长宽比\(aspect\)（近平面的长和宽的比）
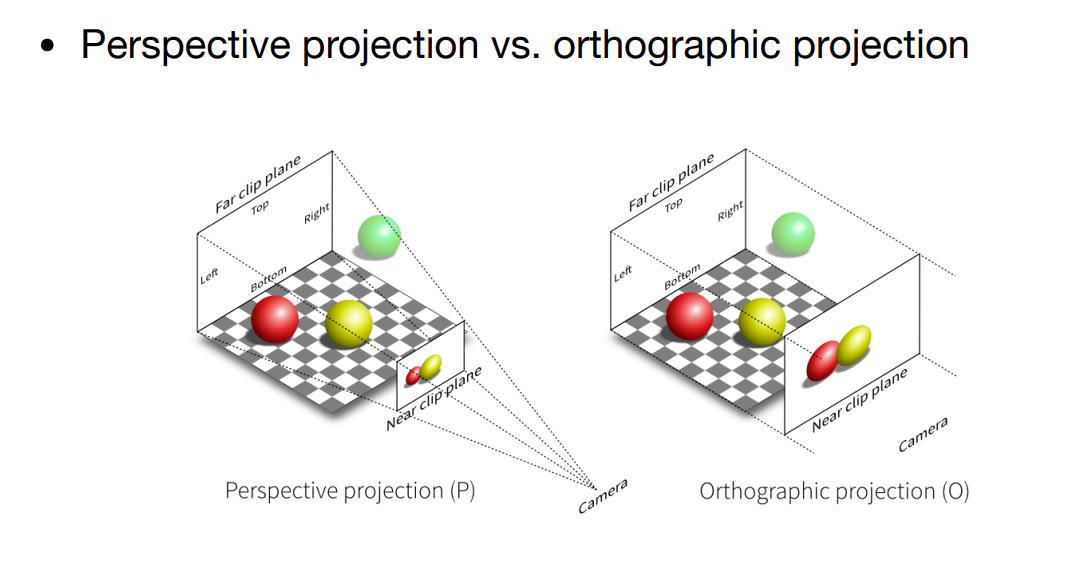
正交投影 vs 透视投影
正交投影是将相机放在无限远的位置上，打出来的是平行光，相同的物体不论距离，呈现的大小一样。 透视投影是将相机放在一个点上，符合近大远小的特点。
思考题
对于中间平面的点，再经过“挤压变换”后，z轴的坐标是会更靠近近平面还是远离近平面？
其实带入点\((x, y, z, 1), (n < z < f)\)，得 \[ M_{persp->ortho}^{(4*4)} * \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} nx \\ ny \\ (n+f)z-nf \\ z \end{bmatrix} == \begin{bmatrix} nx/z \\ ny/z \\ n+f-\frac{nf}{z} \\ 1 \end{bmatrix} \] 将“挤压变换”后得到的z轴坐标与原本的z作差，得 \[ \begin{align*} n+f-\frac{nf}{z} - z & = \frac{nz+fz-nf-z^2}{z} \\ & =\frac{(z-n)(f-z)}{z} > 0 \end{align*} \] 因此，经过“挤压变换”后，z轴的坐标是会远离近平面，靠近远平面。
MVP变换
- Model Transformation（放置物体）
- View Transformation（放置相机）
- Projection Transformation
Projection Transformation
- 正交投影（从长方体变成\([-1, 1]^3\)）
- 透视投影（从截头锥体变成\([-1, 1]^3\)）