Games101-Lecture5-6（Rasterization）学习笔记

发表于 更新于 分类于 本文字数： 3.1k 阅读时长 ≈ 3 分钟

本章内容

在上章的Transformation中，我们得知了MVP变换，将物体变换到了\([-1,1]^3\)的区间内，接下来就需要将物体画在屏幕上，本章将讲述图形学的Rasterization（光栅化）。

前言

屏幕

  • 可以看作一个二维数组
  • 数组的每个元素都是像素
  • 一种典型的光栅成像设备

光栅化

可以理解为在屏幕里画出图像。

像素

  • 在此我们认为，像素是一个一个小的方块，一个小方块颜色是唯一的
  • 一个像素可以表示不同的颜色，由红、绿、蓝三原色混合（RGB）

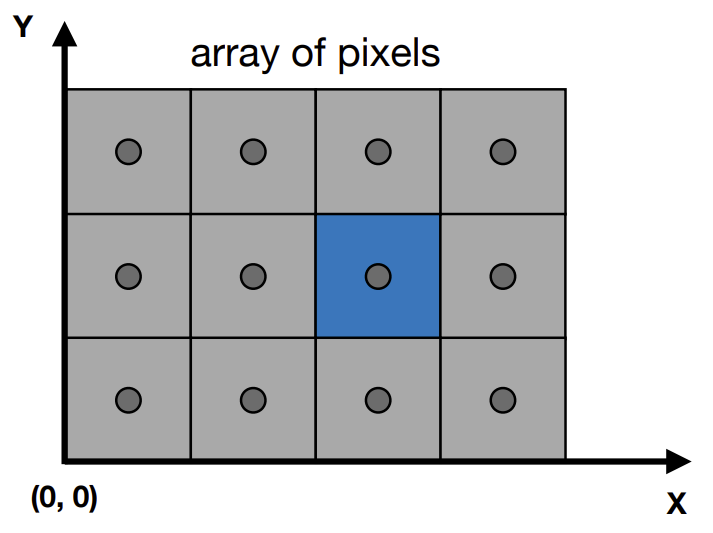
屏幕的空间

  • 屏幕左下角为原点
  • 每个像素都可以通过坐标\((x,y)\)来表示，其中\(x, y\)都是整数
  • 像素的区间从\((0,0)\)到\((width-1, height-1)\)
  • 像素\((x,y)\)的中心在\((x+0.5,y+0.5)\)
  • 屏幕覆盖范围为\((0,0)\)到\((width, height)\)

从正则立方体\([-1,1]^3\)变换到屏幕

  • 暂时忽略z轴

  • 将\(xy\)的\([-1,1]^2\)变换到\([0,width]*[0,height]\)

  • 视口变换，先将高度和宽度从2拉伸至\(width,height\) \[ M_{viewport} = \begin{bmatrix} \frac{width}{2} & 0 & 0 & \frac{width}{2} \\ 0 & \frac{width}{2} & 0 & \frac{width}{2} \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \]

帧缓存区

内存中一个用来光栅化展示的区域

三角形——基本形状图元

  • 最基础的多边形
  • 可以组成其它多边形
  • 保证在同一个平面
  • 很容易区分三角形的内外区域
  • 知道一个三角形和它内部的一个点坐标，可以通过插值的方式，使其颜色达到渐变的效果

输入：投影在屏幕上的三角形顶点的位置 输出：一组近似三角形的像素值

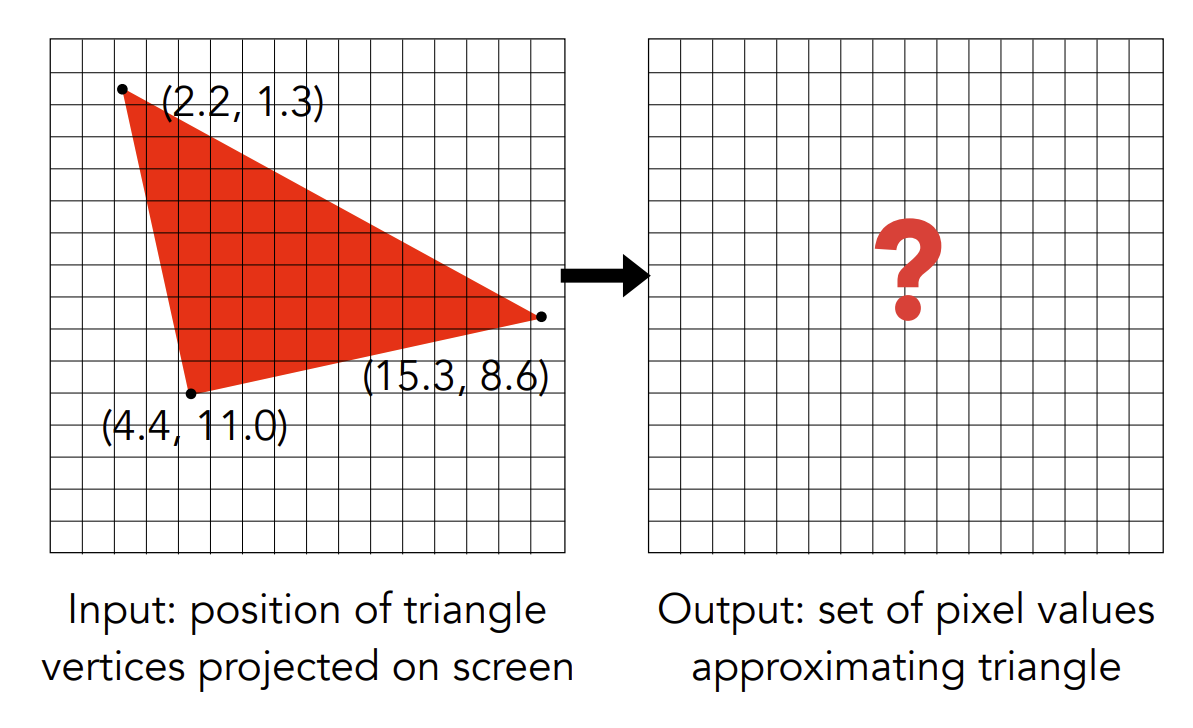
一个简单的光栅化方法

  • 通过采样的方法来进行光栅化，给定一个连续的函数\(f(x)\)，在不同的位置求得像素值

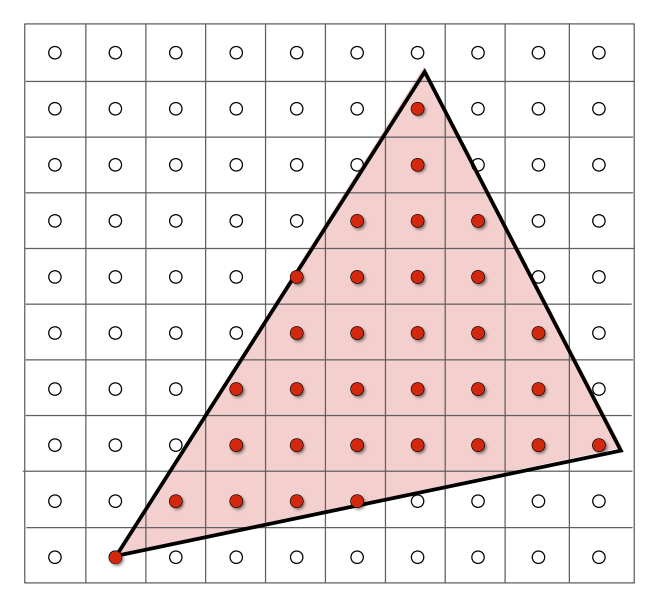
  • 如果像素中心在三角形内，就进行采样

  • 定义\(inside(tri, x, y)\)，\(inside(t,x,y)=\begin{cases}1, &点(x,y)在三角形t内\\0，&点(x,y)在其它区域\end{cases}\)，可以通过叉积判断

1
2
3
for (int x = 0; x < xmax; ++x) 
 for (int y = 0; y < ymax; ++y) 
 	image[x][y] = inside(tri, x + 0.5, y + 0.5);
  • 对于边界上的点，可以自己定义一个规则
  • 使用包围盒（Bounding Box），只有包围盒内的像素才需要考虑采样，可以降低开销

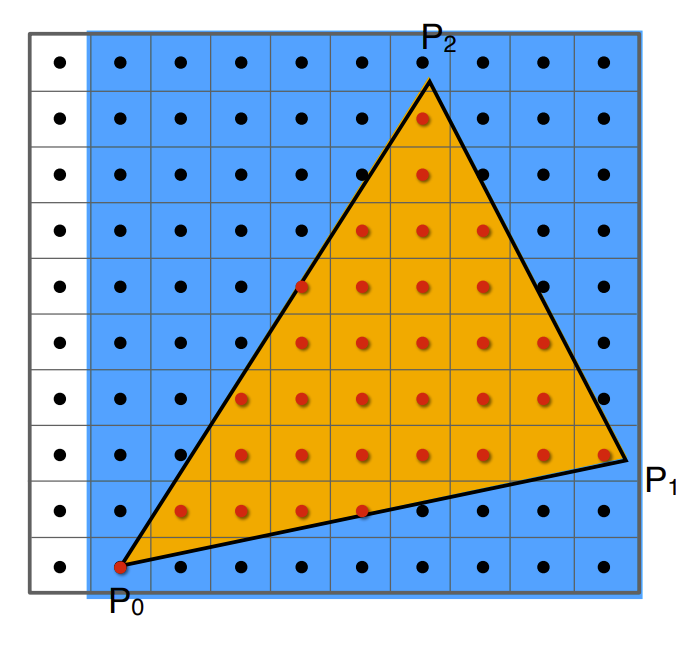
  • 标记三角形最左和最右的坐标，从左到右进行遍历，适合细并且旋转了一定角度的三角形

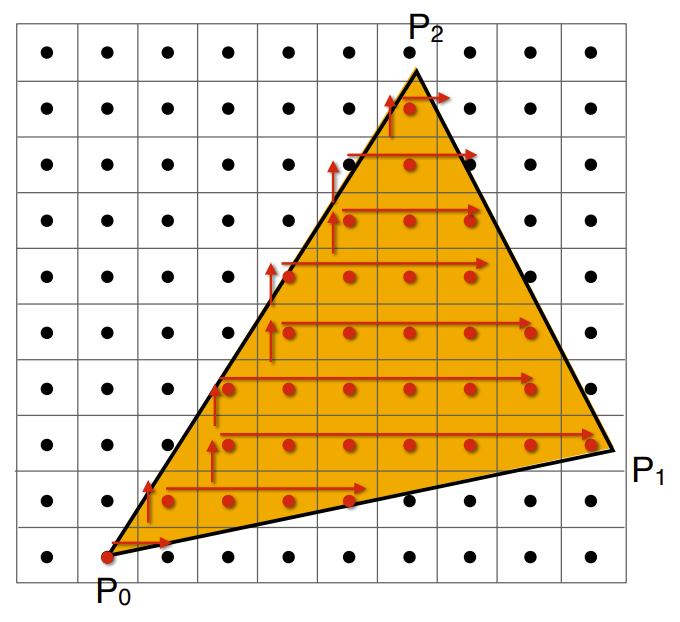
  • 但是，采样会产生锯齿（走样）

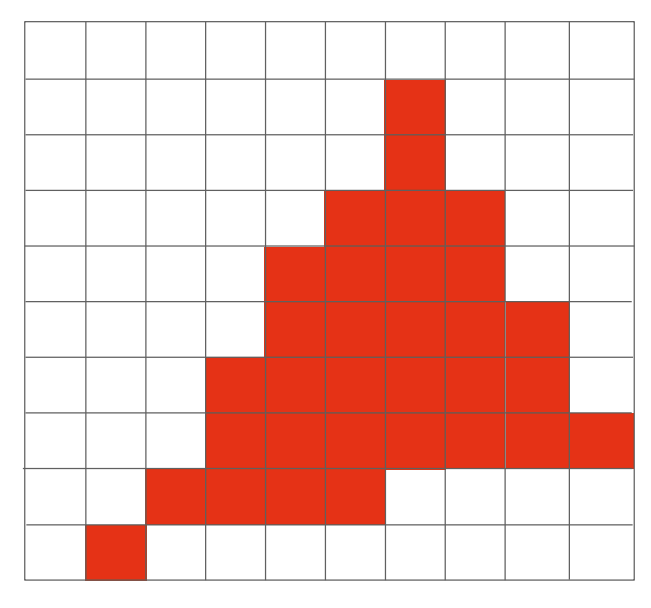
反走样

在采样之前做个模糊（滤波），然后再做采样

频域

傅里叶变换

傅里叶变换将信号分解为频率

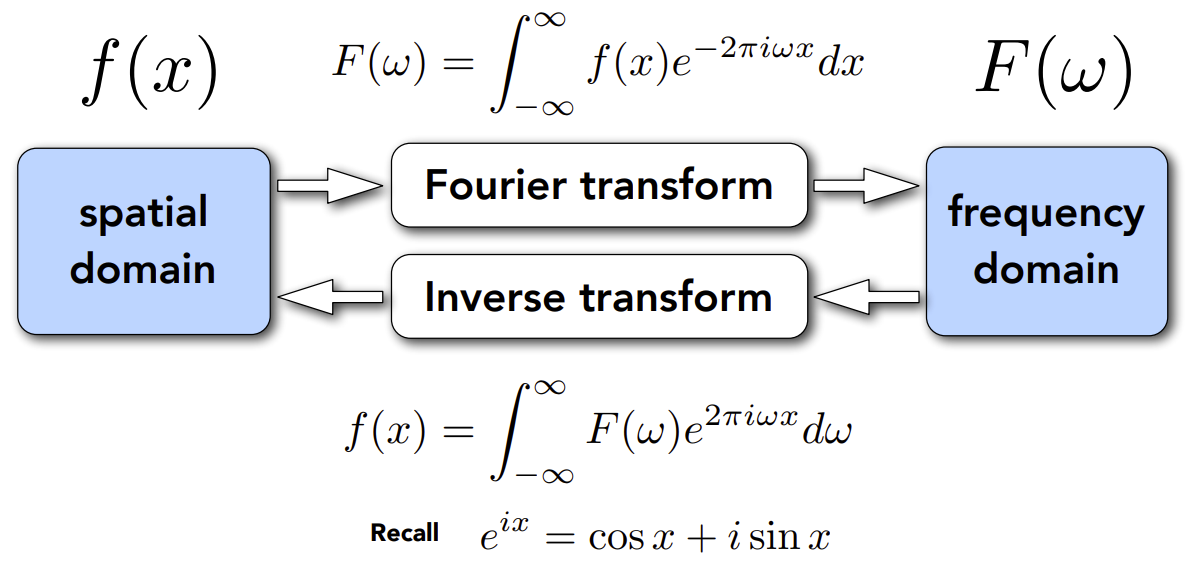
走样的定义

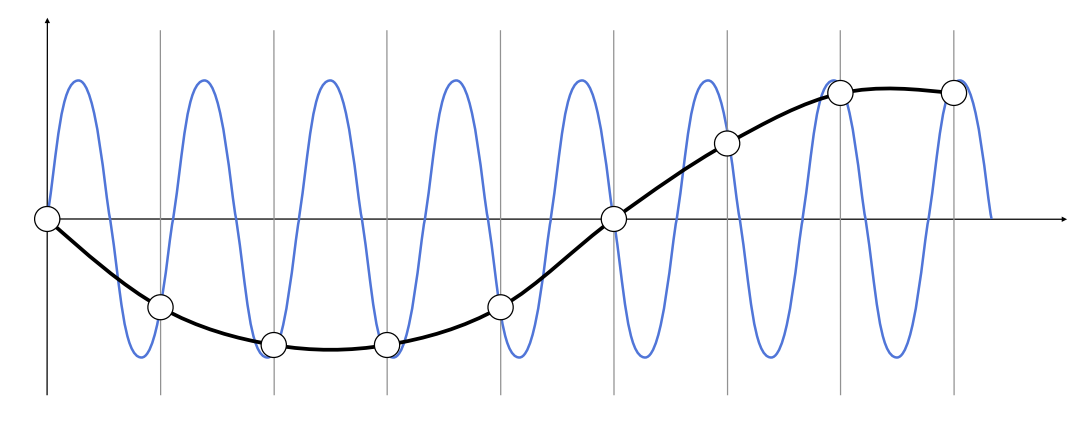
欠采样会产生频率混淆。 对于下面这幅图，图中是高频的信号函数，但是对于我们采样率不足，看起来很像是低频信号，因此无法区分两个频率。

滤波

定义

去掉一些频率的内容。

可视化图像的频率内容

从图像变换的空间（左图），变成了频率变换的空间（右图）。 右图，中心定义为最低频的区域，周围定义为高频的区域，从中心到周围，频率会越来越高，用亮度来表示不同频率的位置上的信息。 如右图所示，右图的大多数信息集中在低频上。

右图水平和竖直两条线产生的原因：我们在分析一个信号的时候，会认为它是一个周期性重复的信号，但是对于一张图片，它并不是周期性重复的内容，所以我们就认为，当到了图片右边界的时候，会重复左边的内容，相当于水平方向和竖直方向放了无数张图。而大多数情况下，图像的右边界和左边界不会完全一致，因此在这条边界上会发生剧烈的信号变化，会产生一个极其高的高频，于是就会产生这两条线，本章讨论忽略这两条线。

傅里叶变换能让我们看到图像在不同频率的样貌，称为频谱。

高通滤波

去除低频的信号，只剩下高频信息，可以看到物体的边界。 因为边界位置本身就会发生剧烈的变化，这就是高频信息，所以它会被留下。

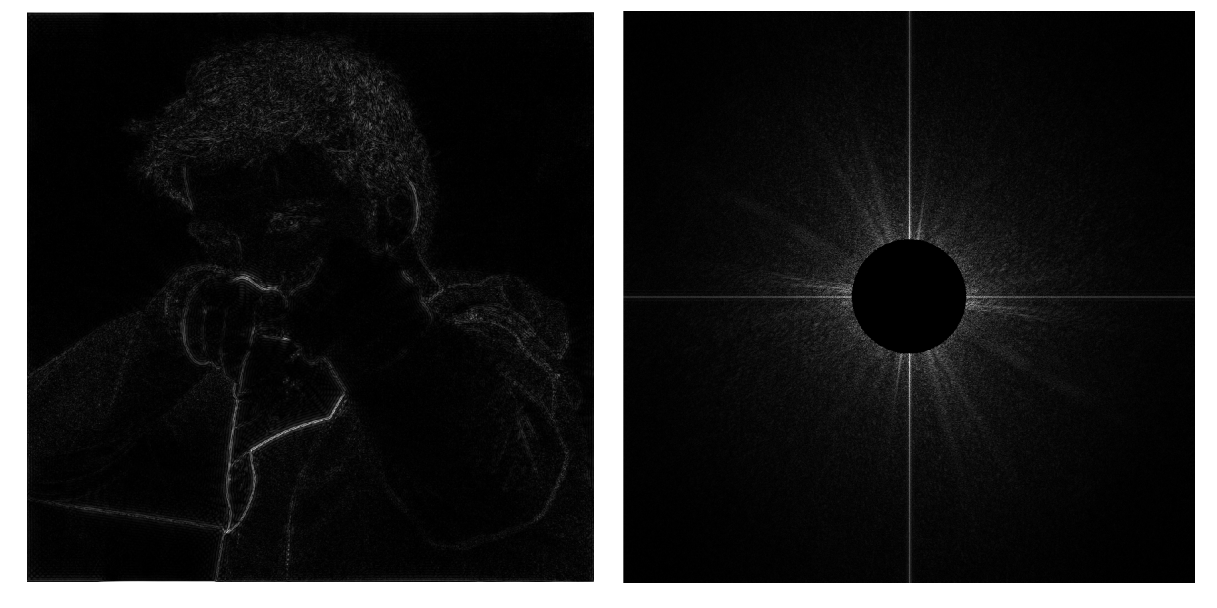
低通滤波

去除高频的信号，只剩下低频信息，边界被去掉，因此图像会变模糊。

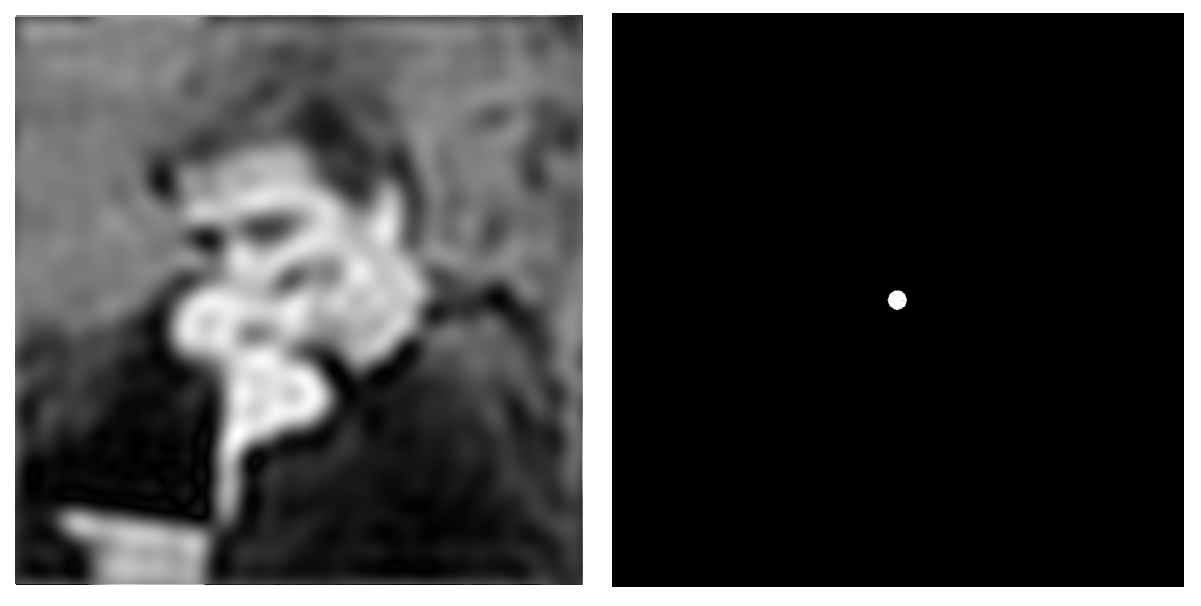
同时去掉高频和低频信息

同时去掉高频和低频信息，会得到一些不是很明显的边界特征。

卷积（平均）

作用在一个信号上，用某一种滤波器，进行卷积操作，得到最终结果。（这不是数学上的卷积定义，而是图形学里简化后的定义，感觉和相关差不多）

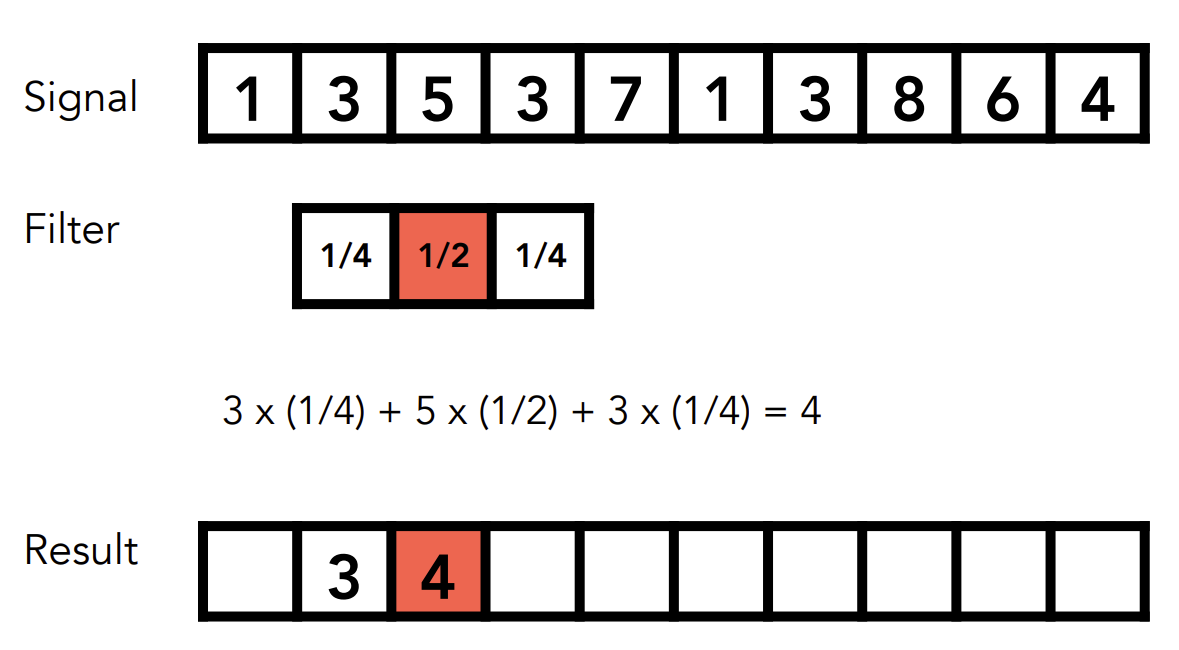
定理

时域上，如果想对两个信号进行卷积，对应到两个信号的频率上，是两个信号的频率的乘积。（卷积操作和乘积操作接近）

实现卷积的两种方法

方法一

  • 直接用滤波器对图进行卷积操作

方法二

  • 先用傅里叶变换将图变换到频域上，卷积的滤波器也变换到频域上
  • 将两者相乘，得到频域的结果
  • 再把结果逆傅里叶变换到时域上

下图为两种方法实现低通滤波。

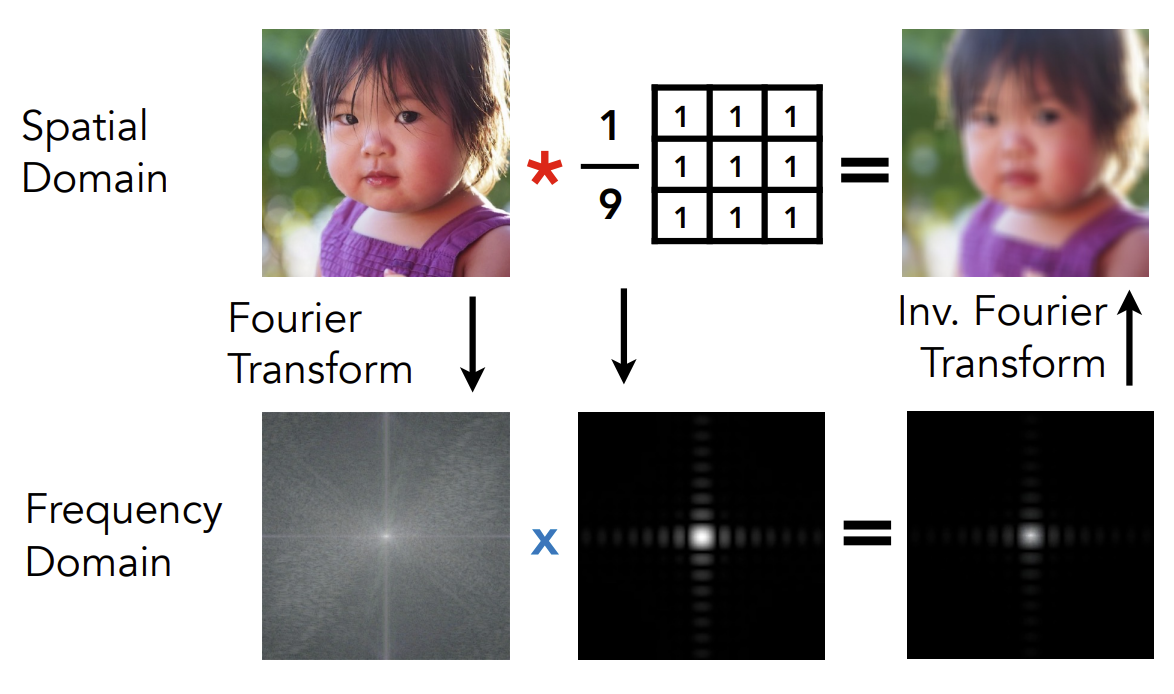
采样（重复频率的内容）

如下图所示，左边是时域，右边是频域。

给一个原本的信号(a)，乘以(c)冲击函数（部分点有值），留下信号上的若干点，得到结果(e)。 时域上的乘积等于频域上的卷积。 (b)卷积(d)得到(f)

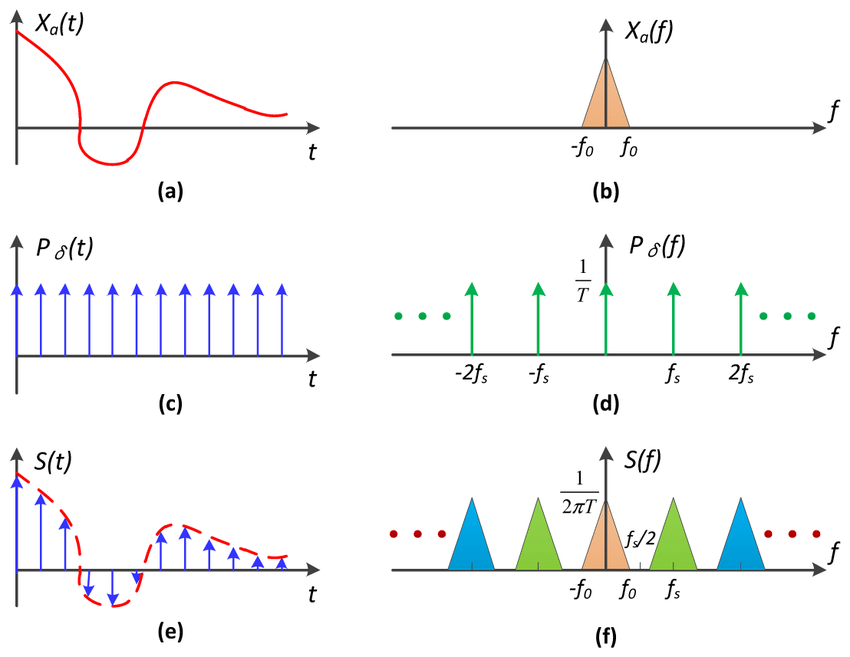
走样（频率的混合）

频率的频谱在经过平移或复制粘贴后，发生了混合（混叠）

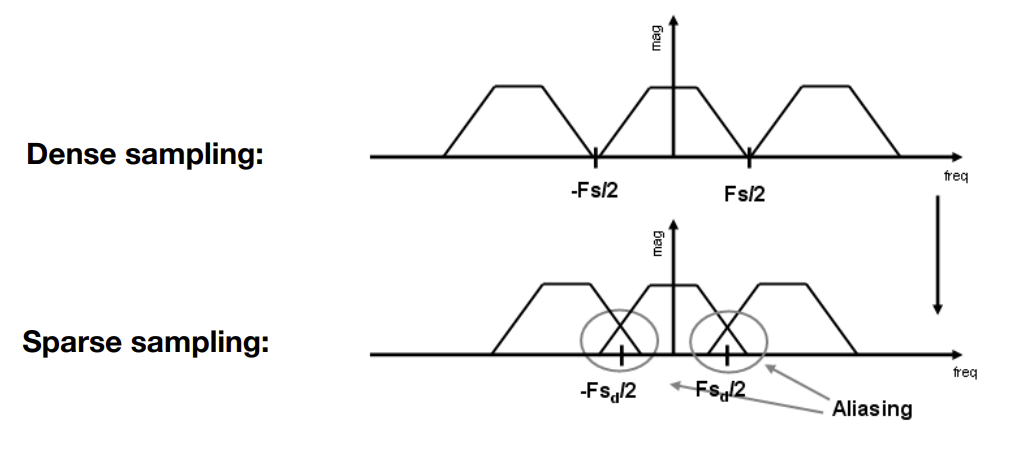
如何减少走样的错误

方法一：增加采样率（终极解决方法）

  • 使用更高分辨率的显示器

方法二：反走样

  • 先做模糊操作（低通滤波），再做采样

如图所示，通过低通滤波，高频会被截断，因此可以减少混合（混叠）的现象。

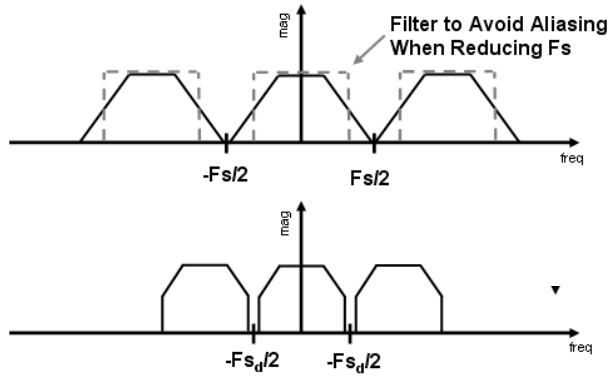
通过超采样（MSAA—MultiSampling Anti-Aliasing）进行反走样

步骤

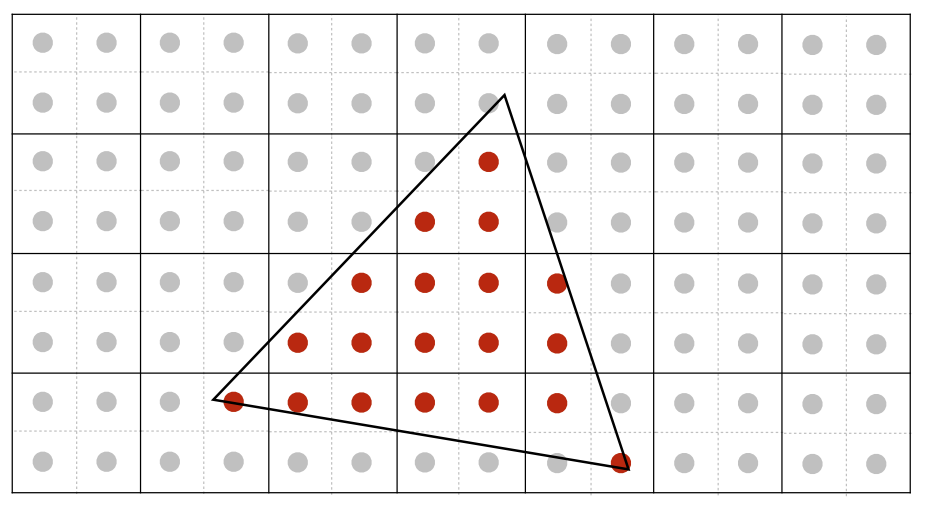
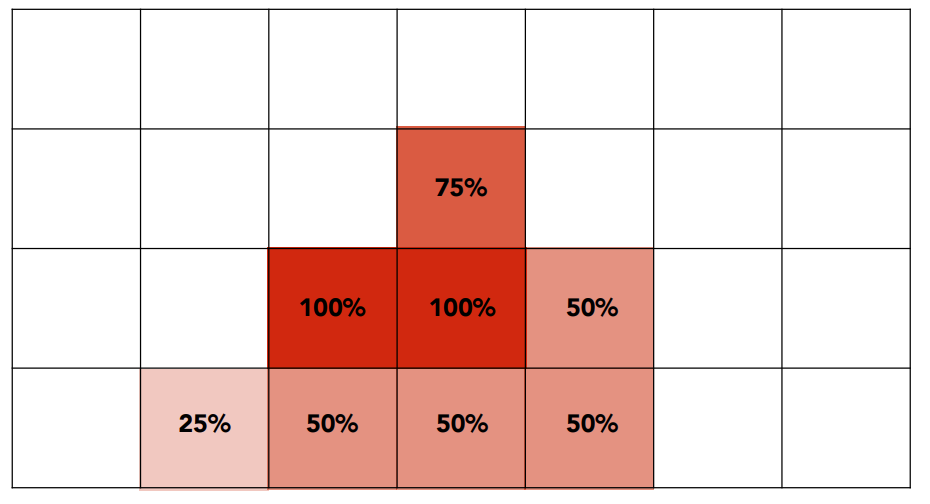
我们认为把一个像素可以再细分为很多个次像素，判断这些小像素是否在三角形内，然后再把判断的结果进行平均，就能得到一个近似结果。如下图所示，每个像素被再细分为2*2的次像素，根据三角形与每4个小像素的覆盖情况，可以得到0、25%、50%、75%、1的平均，以上是模糊操作，最后直接采样就行。

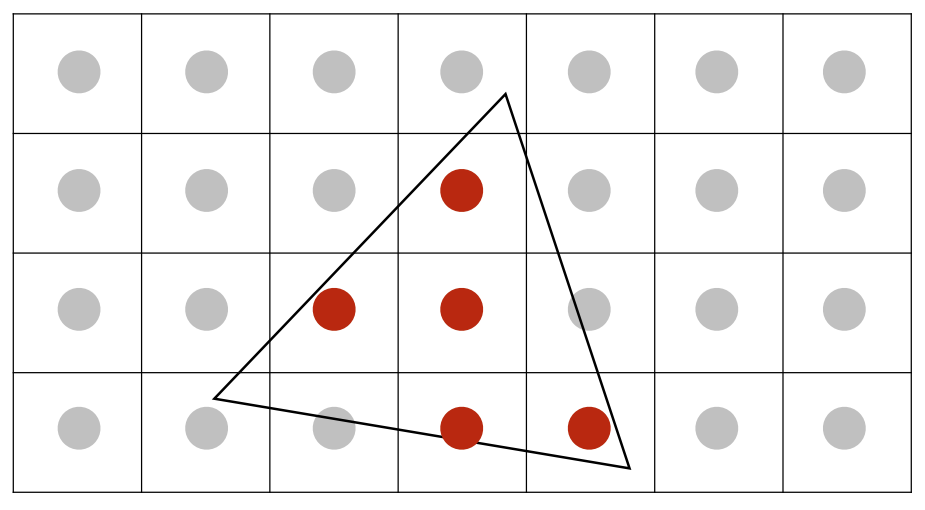
总结

代价

  • 抗锯齿提高了开销

其它方法

  • FXAA（Fast Approximate AA），生成有锯齿的图片之后，对锯齿进行处理，替换成没有锯齿的边界
  • TAA（Temporal AA），将上一帧感知到的结果应用到当前帧，相当于把MSAA对应的这些样本分布在时间上，并且在当前帧没有引入任何额外的操作。

超分辨率

  • 可以理解为2k的片源放到4k的显示器上，将其恢复成更高分辨率
  • 从低分辨率到高分辨率
  • 本质还是采样率不足的问题
  • 对于高分辨率下未知的像素点，使用深度学习的方法进行猜测，DLSS (Deep Learning Super Sampling)

深度测试（Z-buffering）

油画家算法

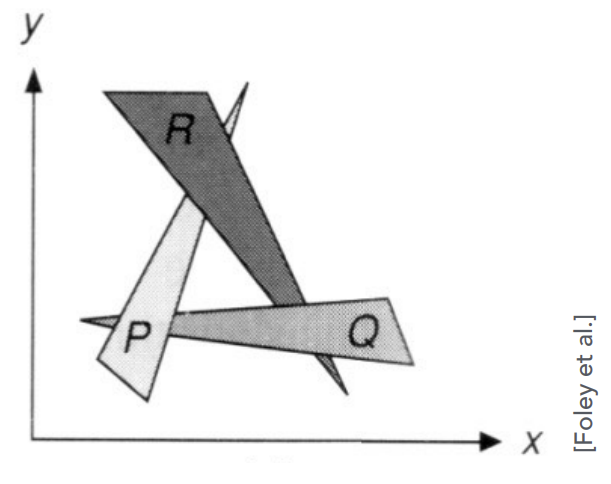
从远到近，让近处的物体覆盖远处的物体。开销为O(n log n)，但是对于相互覆盖的物体无法判断，如下图。

Z-Buffer

为了解决上述问题，这里使用Z-Buffer，思想如下

  • 存储每个像素当前的最小z值
  • 需要用一个额外的缓存区来存储深度信息，始终同步生成两个缓存区
  • 帧缓存区存储颜色值
  • 深度缓存区存储深度，维护遮挡信息
  • 简单起见，我们假设z始终为正，z越大表示离相机越远

1
2
3
4
5
6
7
8
//每个像素深度的初始值为无限大
for (each triangle T)
    for (each sample (x,y,z) in T)
        if (z < zbuffer[x,y]) // closest sample so far
            framebuffer[x,y] = rgb; // update color
            zbuffer[x,y] = z; // update depth
        else
                   ; // do nothing, this sample is occluded

总结

  • 深度缓存复杂度为O(n)
  • 几乎应用在所有的GPU硬件中