Games101-Lecture7-9(Shading)学习笔记
本章内容
在之前的章节,我们已经学习了视图变换、投影变换,将物体投影到\([-1,1]^{3}\)的区间上,再进行光栅化,本章将讲述Shading(着色)部分。
Blinn-Phong模型(经验模型)
- Specular highlights(高光)
- Diffuse reflection(漫反射)
- Ambient lighting(环境照明)

计算在特定阴影点(shading point)反射到相机的光,输入包括以下内容,以下向量都看作是单位向量,注重方向
- 观察方向,\(\vec{v}\)
- 法线方向,\(\vec{n}\)
- 光照方向,\(\vec{l}\)(对每束光)
- 表面参数等(颜色、亮度)
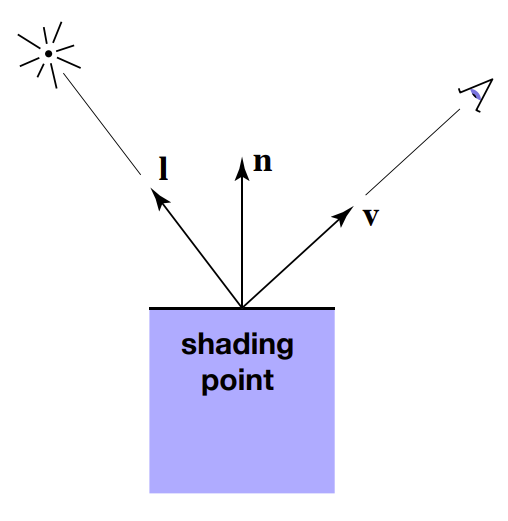
着色具有局部性,我们只管当前光线打到该位置的着色,而不考虑阴影等因素。
漫反射
当光线打到物体的某一个点的时候,光线会均匀地反射到各个不同的方向。
- 光均匀地向各个方向散射
- 表面颜色是相同的所有观看方向
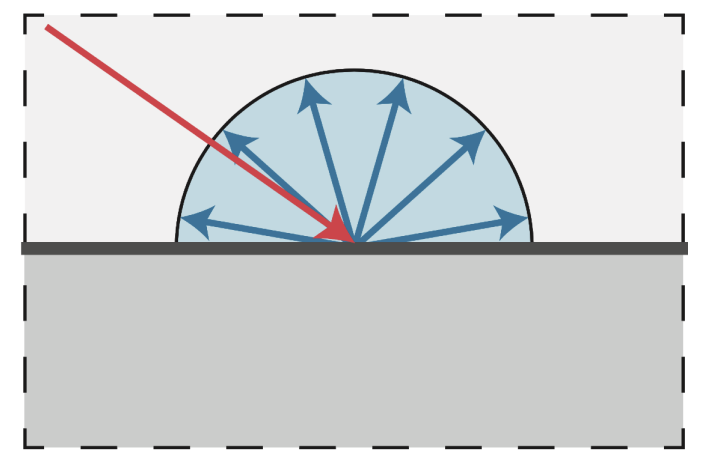
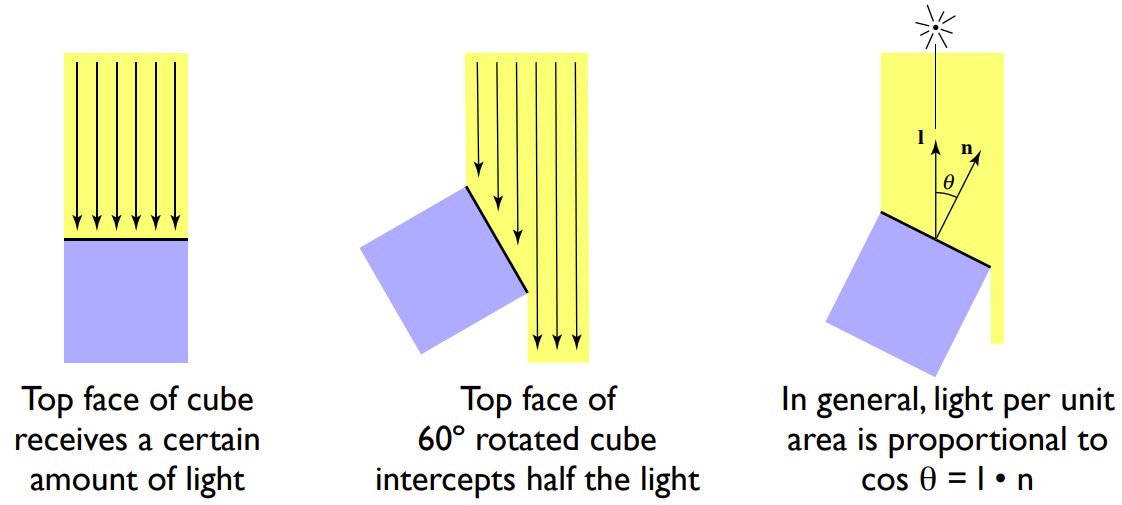
相同的光线以不同的角度打到相同的物体上,呈现的效果不一样。
- Lambert余弦定律:接收到的能量与光线方向、法线方向间的夹角的余弦成正比
光线衰减
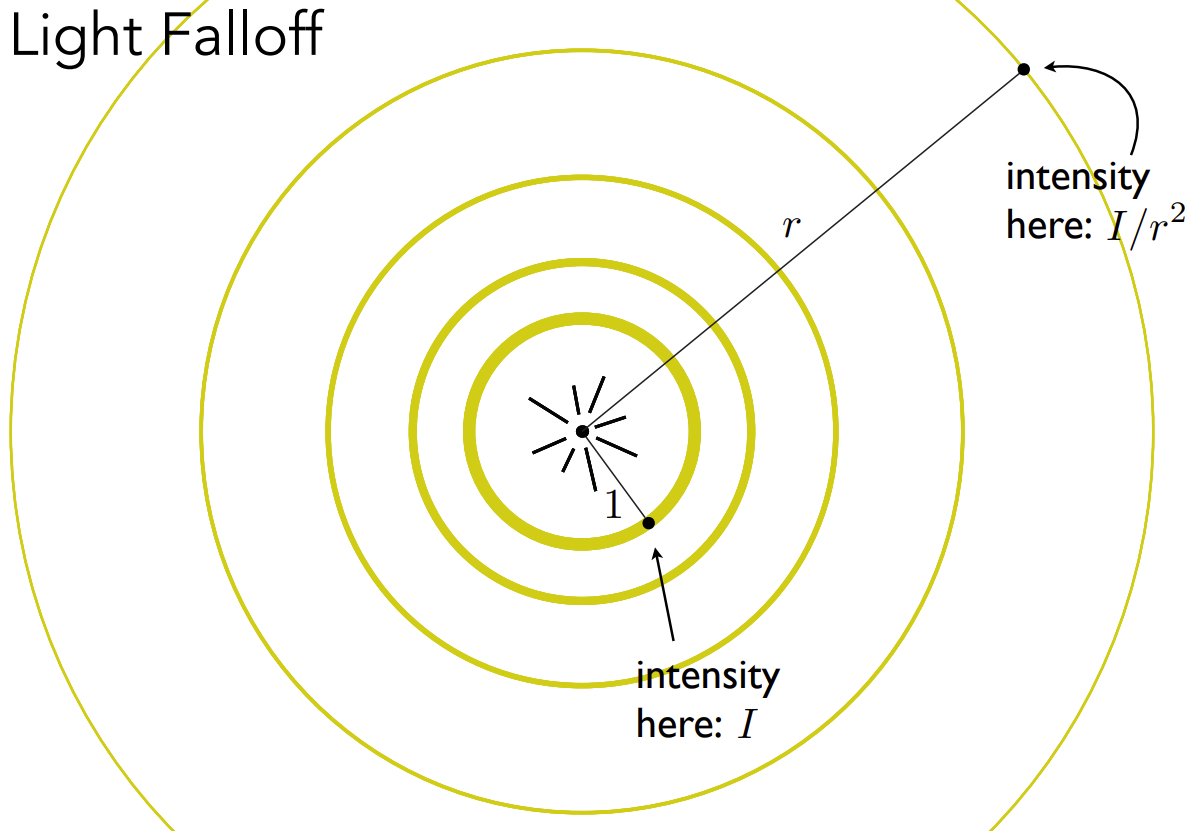
- 点光源不断往四面八方辐射能量
- 在某一个时间,能量集中在某一个球壳上
- 能量守恒,每个球壳上的能量是一样的
- 同时,外侧的球壳表面积更大,相同能量下,外侧球壳上某一个点的能量更少
- 定义点光源单位距离1的位置的光强度是\(I\),距离为r的位置的光强度是\(I/r^2\)
Lambert漫反射
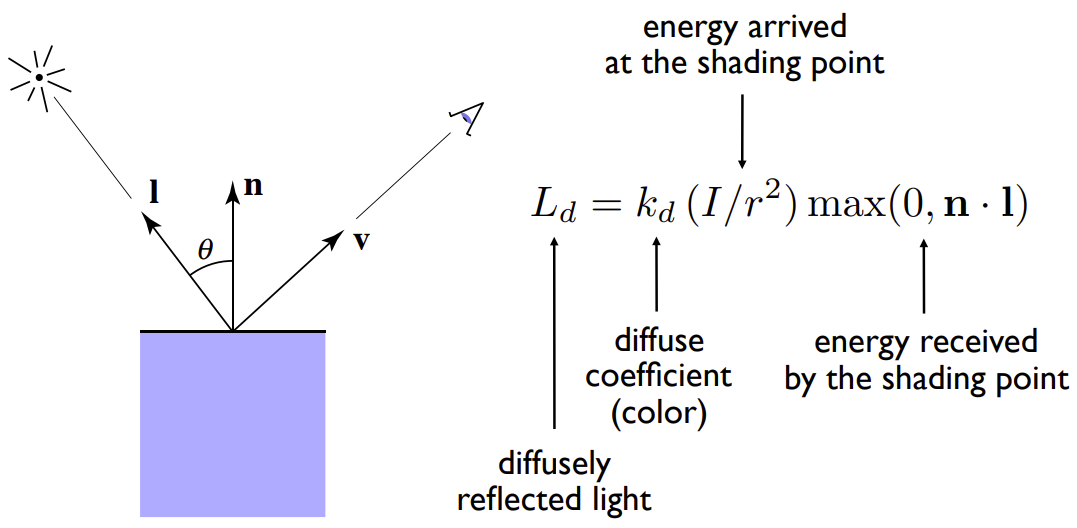 \[
L_{d} = k_{d}*(I/r^2)*max(0,\vec{n}·\vec{l})
\]
\[
L_{d} = k_{d}*(I/r^2)*max(0,\vec{n}·\vec{l})
\]
\(k_d\)表示物体材质的漫反射系数,表示物体吸收光的能力,1表示完全不吸收能量,0表示表面是黑的,所有能量都被吸收了,没有光线漫反射
\(r\)表示光源与shading point的距离
\(\vec{n}·\vec{l}\)表示光线方向与法线方向夹角的余弦,为了防止出现光源从下方达到上方(这里考虑漫反射,不考虑折射),所以不考虑负数的情况
这个公式意味着,不管我们从哪个角度观察shading point,得到的漫反射能量完全一样,这也符合生活现象,漫反射与观察方向没有关系
\(k_d\)系数渐变的漫反射情况

镜面光照
- 高光,平面比较光滑
- 观察方向接近镜面反射方向,会显示出高光,即下图\(\vec{v}\)和\(\vec{R}\)足够接近
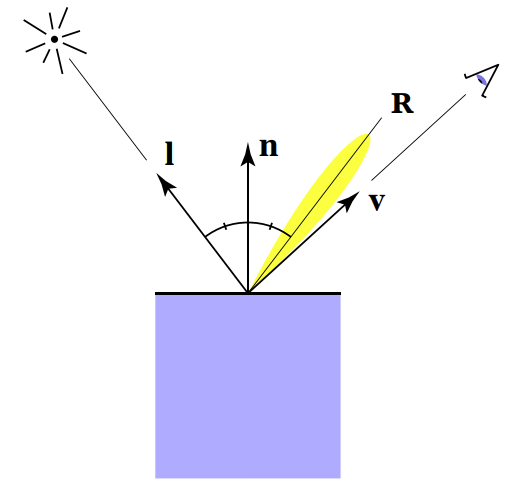
- 在Blinn-Phong中,观察方向和镜面反射方向接近 = 法线方向和半程向量方向接近,如下图,半程向量为\(\vec{h}\),\(\vec{h}\)和\(\vec{n}\)接近反映了上图的\(\vec{v}\)和\(\vec{R}\)接近,通过向量的点乘可以判断是否接近
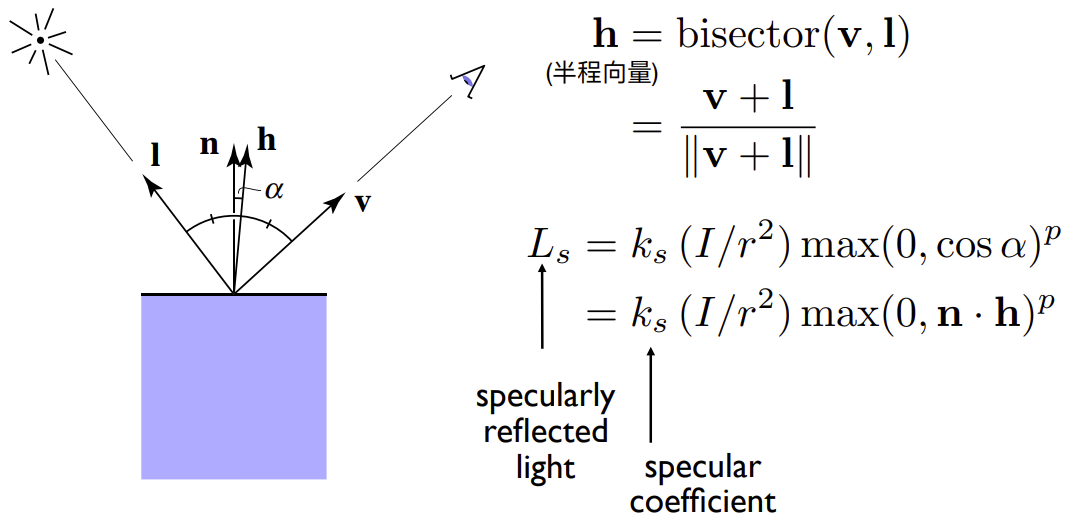
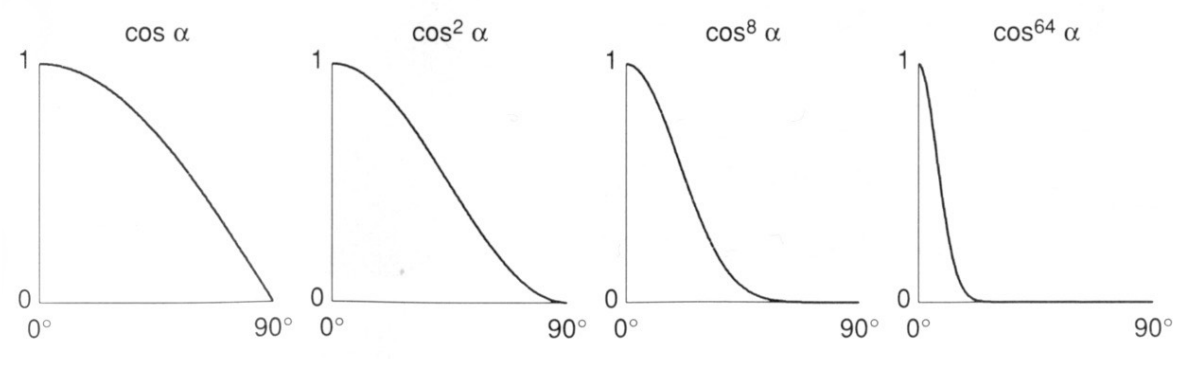
- 增大p使反射波形变窄,因为观察方向和镜面方向夹角很小时,能看到高光,因此是一开始变换就很大,我们可以给它加上幂函数,改变原本的余弦函数形状,p用来控制高光的大小

环境光照
光线通过多次弹射打到空间四面八方的各个点上
来自环境的光永远都是相同的,是一个常数
与观测的远近、方向无关
保证没有地方完全是黑的
如下公式,\(L_{a}\)是反射的环境光,\(k_{a}\)是环境系数,
\[ L_{a} = k_{a}*I_{a} \]
Blinn-Phong反射模型

着色频率
3种不同着色频率结果如下:

平面着色
- 每个三角形是一个平面,将每个三角形的法线求出来,三角形两边做一个叉积可以求出三角形法线,再进行着色,每个三角形使用一个着色结果
- 三角形面是平的,意味着只有一个法向量
- 不适合光滑的表面

Gouraud着色
- 在任意一个顶点上求出它的法线,借此每个顶点进行着色,三角形三个顶点都有颜色后,三角形内部通过插值的方法计算颜色
- 从三角形的顶点插入颜色
- 每个顶点都有一个法线向量

Phong着色
- 三角形每个顶点求出各自法线后,通过插值的方法求出三角形内部各个点的法线,再对每个像素进行着色
- 在每个三角形上插入法线向量
- 计算每个像素的完整着色模型
- 不是 Blinn-Phong 反射模型

着色模型对比
当模型已经足够复杂,有足够多的面的时候,逐像素着色效果不一定比后两者差,还可以减小开销。

计算每个顶点的法线向量
- 最好的方法是从底层几何体中获取顶点法线,即已经知道通过三角形表示什么几何体,然后根据这个几何体计算出顶点的法线
- 否则必须从三角形面推断顶点法线,一个简单的方案,平均周围面法线:任何一个顶点,会被很多面共用,于是我们通过求相邻面的法线的平均作为该顶点的法线,如下公式,面积大的三角形给更大的加权,通过加权平均进行改进
\[ N_{v} = \frac{\Sigma_{i}N_{i}}{||\Sigma_iN_i||} \]
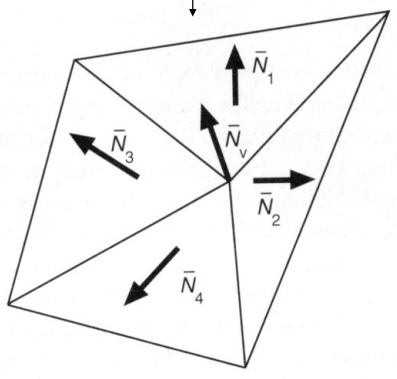
计算每个像素的法线向量
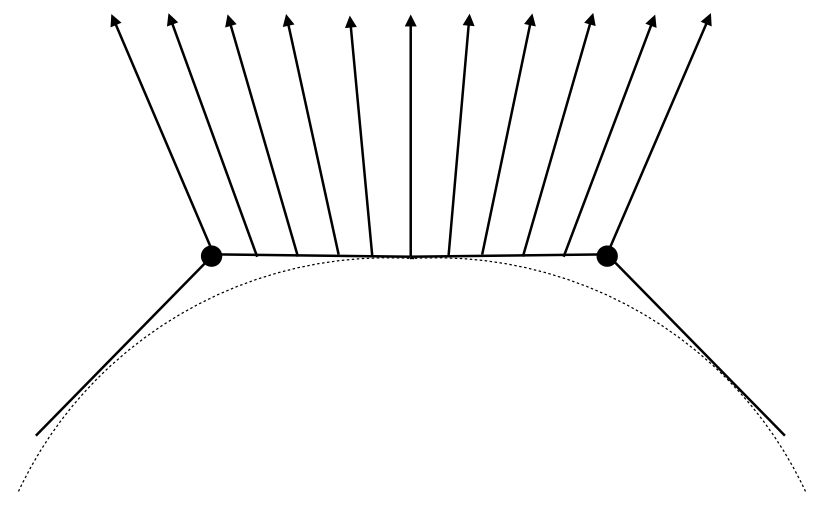
- 通过重心坐标计算(稍后会讲),如下图,已知最左和最右两个顶点的法线,计算中间每个像素的法线向量
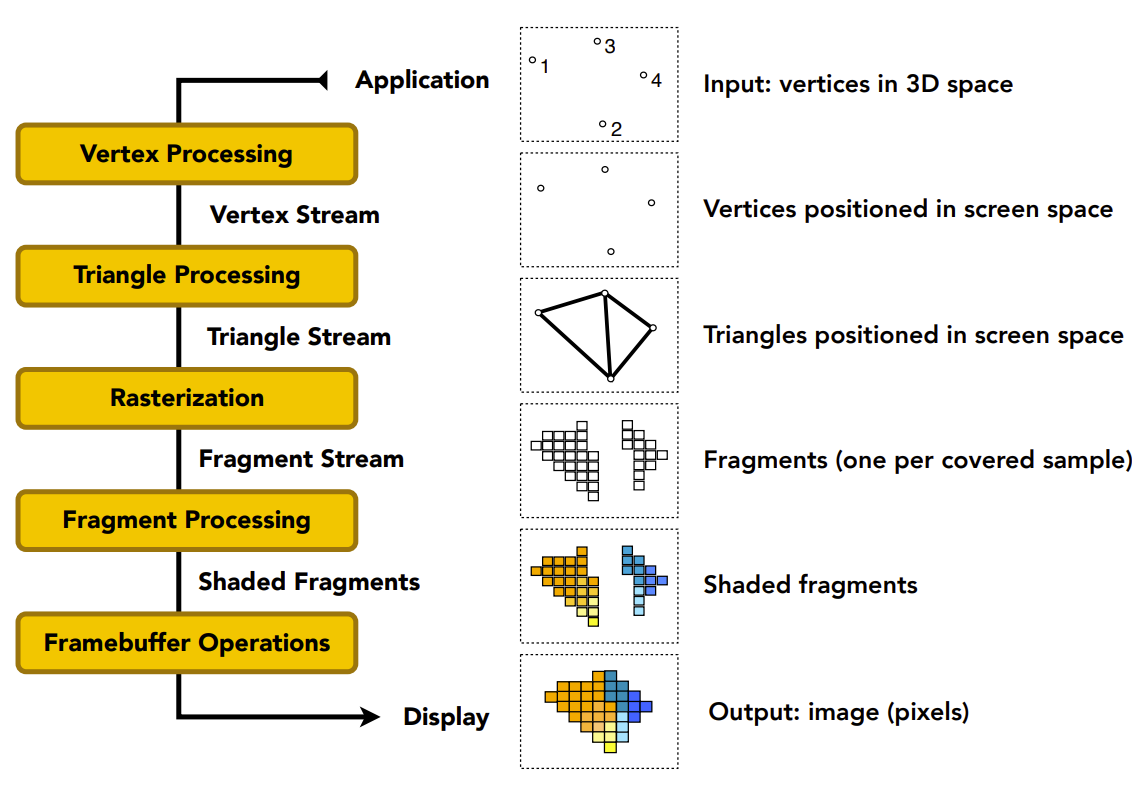
图形管线(实时渲染管线)
流程
与之前在LearnOpenGL学的差不多,流程如下图:
Shader编程
- 程序顶点和片元处理阶段,vertex shader和fragment shader
- 描述对单个顶点(或片元)的操作
- 着色器功能每个片元执行一次
- 输出当前片元屏幕样本位置的表面颜色。
- 此着色器执行纹理查找以获取此时表面的材质颜色,然后执行漫反射光照计算。
纹理映射
- 定义任何一个点的基本属性
- 任何一个三维物体的表面都是二维的
- 可以多次重复使用
如何在三角形内部进行任意属性的插值(重心坐标)
为什么要在三角形内部做插值
- 在顶点指定值
- 获得跨三角形内部平滑过渡的值
在三角形内部插值什么内容
- 纹理坐标、颜色、法线向量
怎么做插值
- 通过重心坐标(Barycentric coordinates)
重心坐标
定义
重心坐标是定义在一个三角形上的,每个三角形有各自的重心坐标。
三角形内部的任意一个点(x,y),都可以被3个顶点的线性组合表示,即下图式子,其中α、β、γ均为非负数。
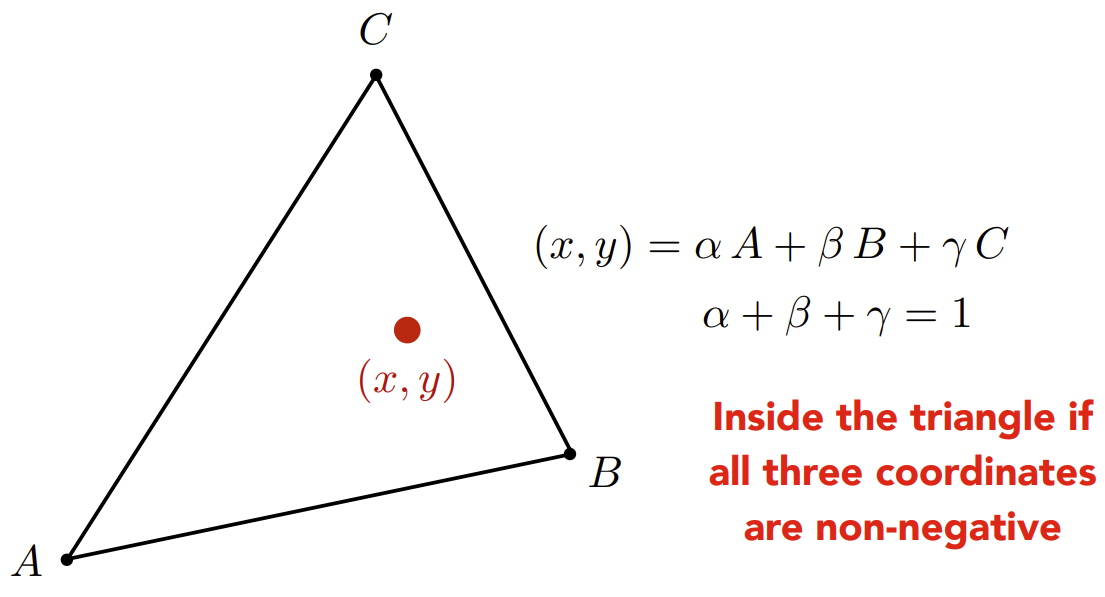
计算重心坐标——几何面积比
将该点与三个顶点各自相连,每个顶点各自对应的三角形占总三角形面积的比例即为系数。
物体的质心的重心坐标是\((\frac{1}{3},\frac{1}{3},\frac{1}{3})\),它将三角形分成等面积的三份。
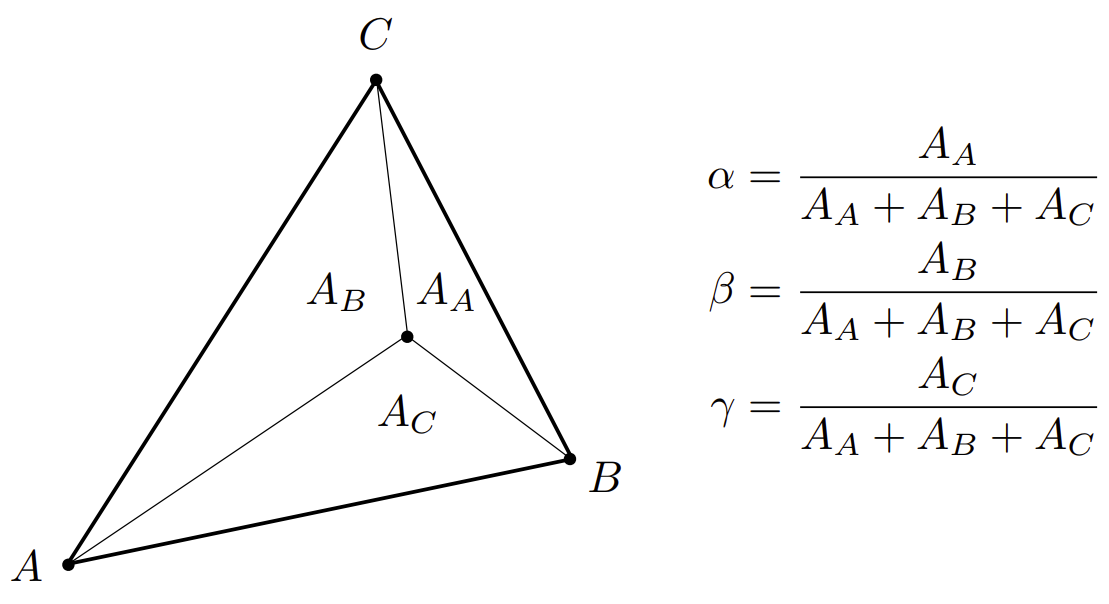
其它插值
通过重心坐标的方法,我们可以应用到颜色、纹理、法线、深度等插值上。
但是存在一个问题,重心坐标不能应用在投影,比如将物体从三维空间投影到二维空间,物体的形状和大小可能会发生改变,因此不能保证重心坐标不变。
因此,如果想插值一个三维空间中的属性,应该取三维空间中的坐标做插值,而不能取投影之后的三角形做插值。
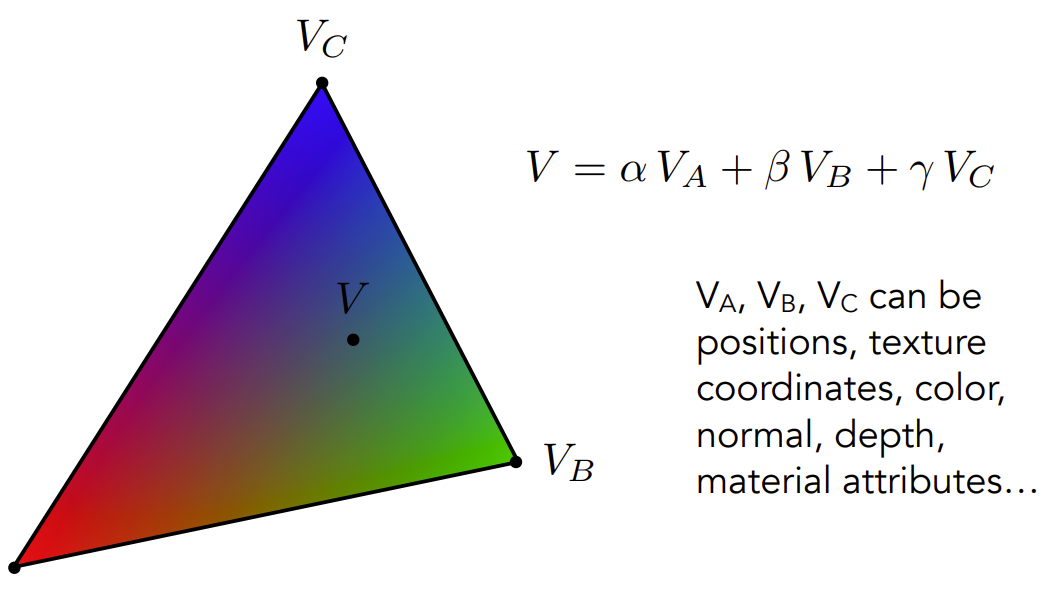
应用纹理
流程

纹理放大
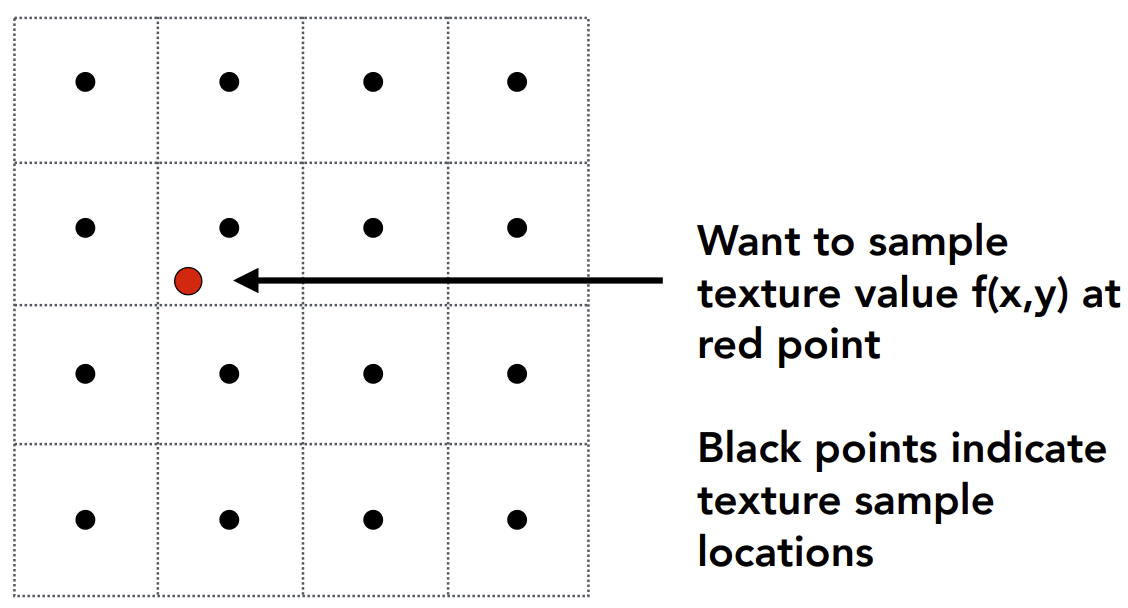
当纹理的分辨率不够,我们将其放大观看时,会出现像素对应的纹理坐标不为整数。
Nearest(四舍五入)
直接取得到的纹理坐标最近的纹理坐标,如下图,取红点右上角的黑点作为纹理坐标。
Bilinear(双线性插值)
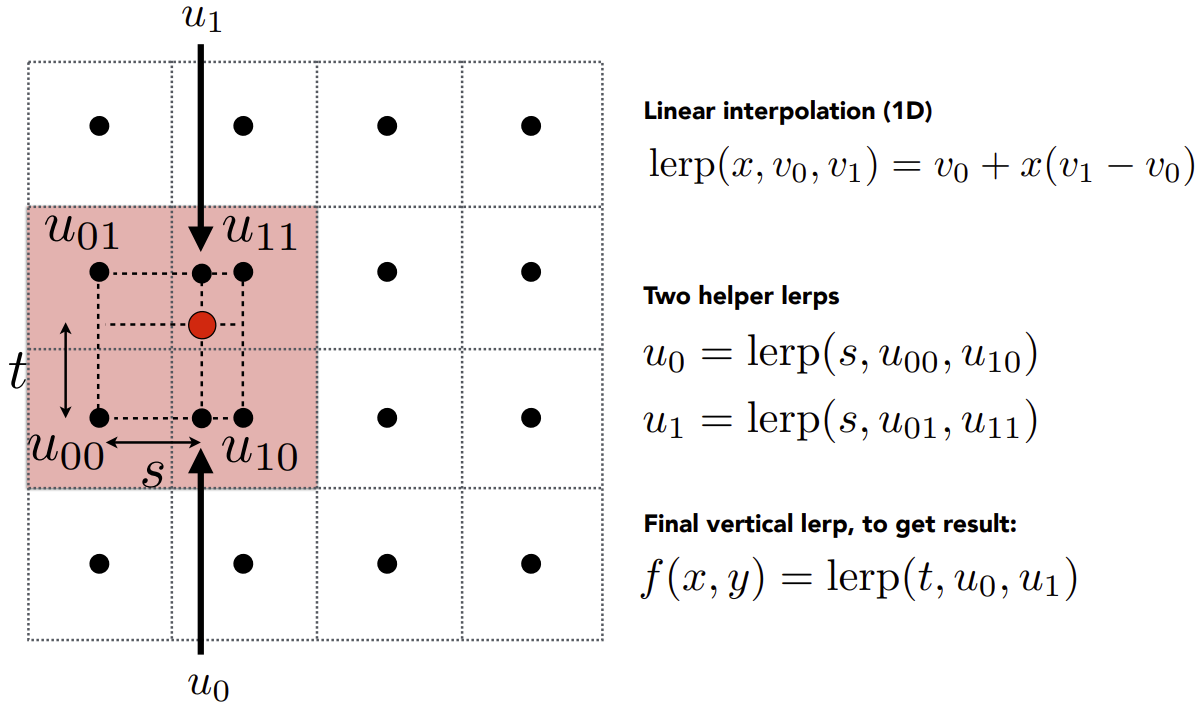
先取计算出的纹理坐标相邻近的四块,我们记\(lerp(x,v_0,v_1)=v_0+x(v_1-v_0)\)表示为线性插值(一维)。
记该点与左边的距离为s,该点与下边的距离为t,通过\(lerp(s,u_{00},u_{10})\)和\(lerp(s,u_{01},u_{11})\)进行插值,得到\(u_0\)和\(u_1\),再利用t对\(u_0\)和\(u_1\)进行插值,\(f(x,y)=lerp(t,u_0,u_1)\),即可得到最终的颜色。
通过双线性插值,可以得到平滑的过渡。
Bicubic
思想与双线性插值类似,但它取的不止4个,而是周围的16个,每次用4个做3次的插值,不是线性的插值。
效果对比

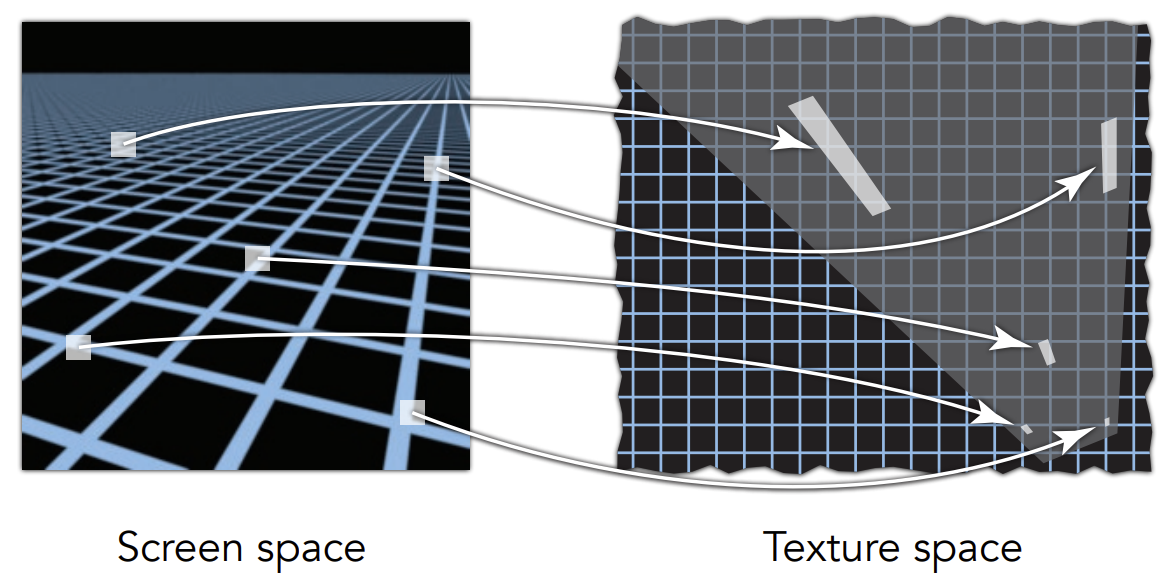
纹理缩小
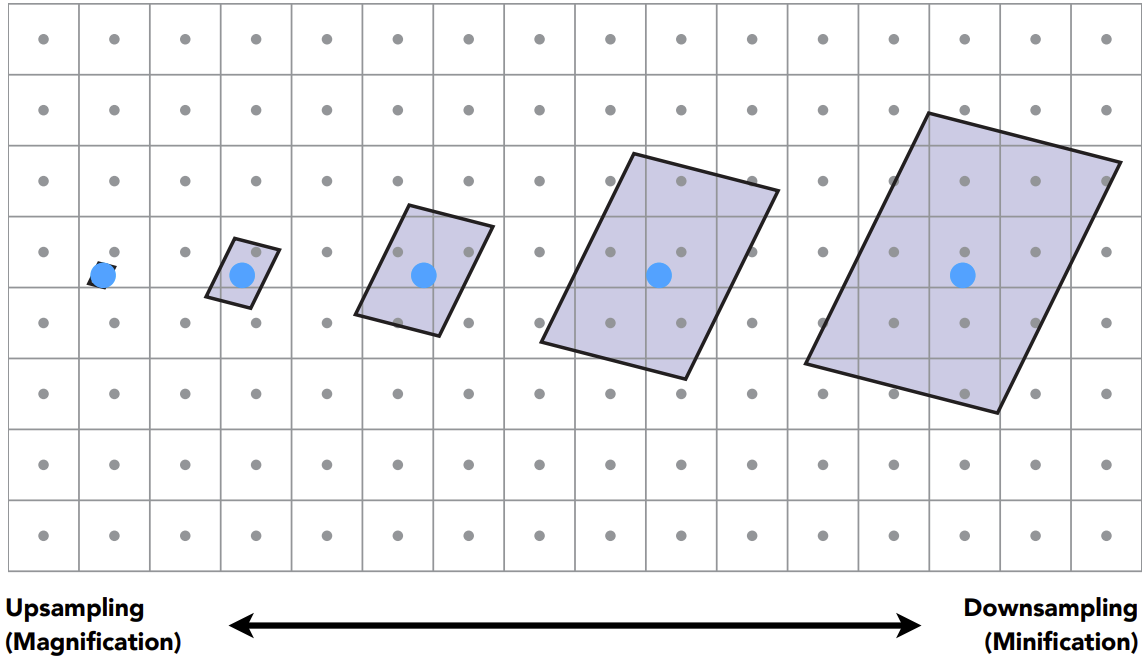
当纹理的分辨率过大,像素对应的纹理太大也是问题,如下图所示。
原图如左边,上方的像素点对应的实际纹理区域很大,如果我们直接用像素点对应的纹理坐标的颜色,会产生如右图的现象,远处出现摩尔纹,近处出现锯齿。

超采样
一个像素点有很多纹理坐标,对这些纹理坐标进行超采样
质量高,但成本高
当高度缩小时,像素足迹中有许多纹素
以像素为单位的信号频率太大
需要更高的采样频率
Mipmap
特点:
- 不采样,但是能够立刻得到一个区域的纹理平均值
- 快、不准确、正方形的范围查询
给一张图,用这张图来生成更多的图,如下图所示,每一张图的边长都是前一张图的\(\frac{1}{2}\),因此后一张图的存储空间都是前一张图的\(\frac{1}{4}\),通过级数求和,\(1+\frac{1}{4}+\frac{1}{16}+...++\frac{1}{4^{n-1}}=\frac{4}{3}\),因此额外的存储空间是原来的\(\frac{1}{3}\)

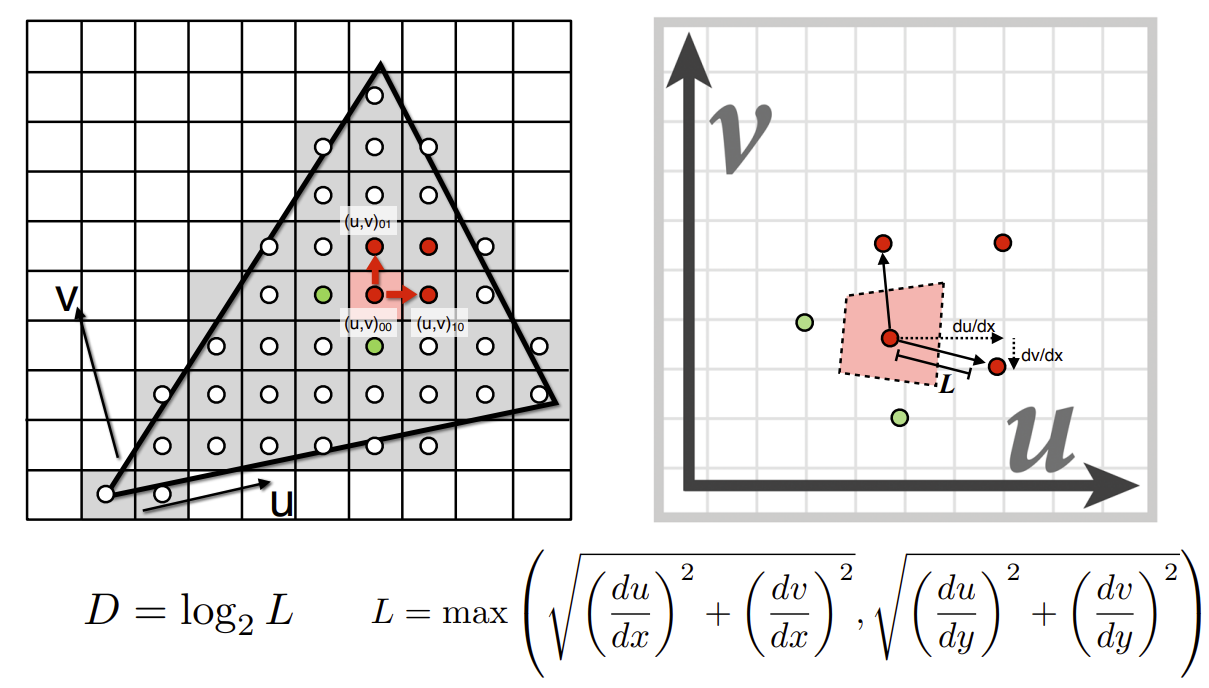
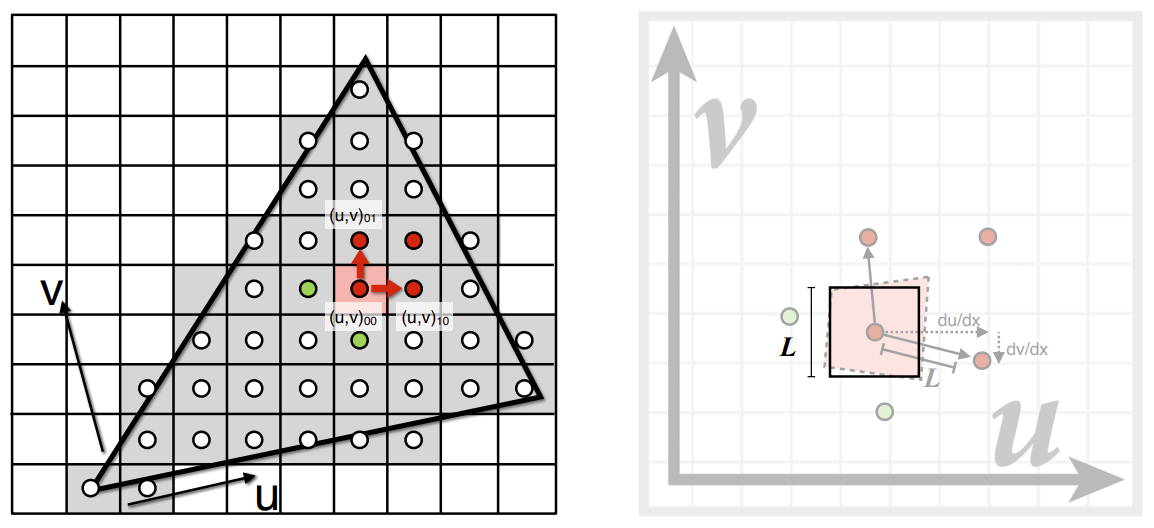
接下来考虑计算像素对应的纹理区域大小。
对于当前像素点,我们除了计算它的纹理坐标外,我们还要计算它相邻点(右边和上面)的纹理坐标,通过它和相邻点的纹理坐标计算,可以得出该像素点的区域大小。
通过求得的L查询该像素点处于第几层的Mipmap,\(D=log_{2}L\),四舍五入。
近处使用低层的Mipmap,远处使用高层的Mipmap。
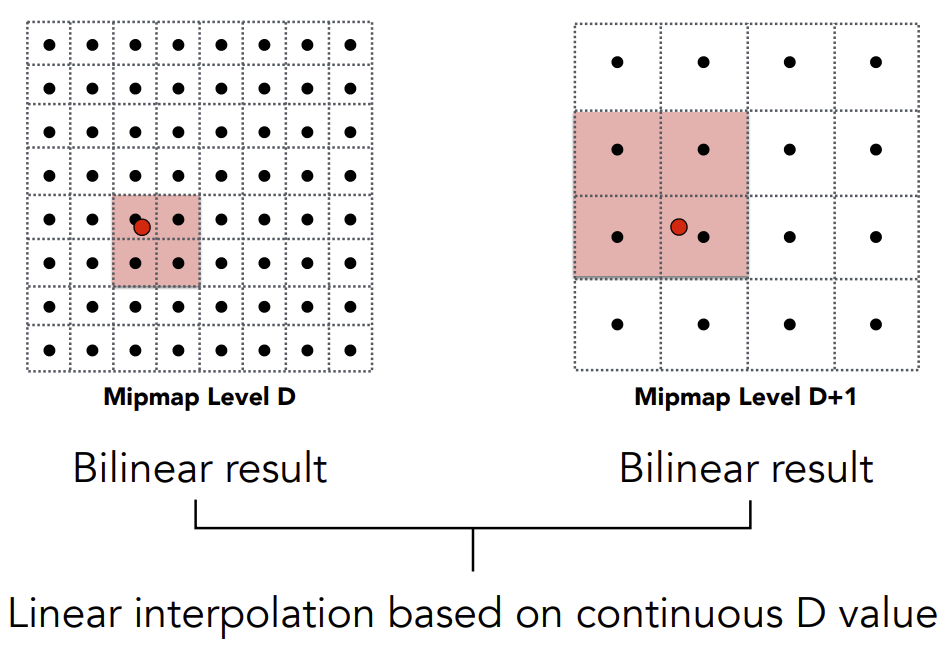
使用Mipmap存在一个问题,相邻的一块区域,如果出现一个在第1层,一个在第2层,可能会产生撕裂感,我们希望得到类似1.8层(某个非整数)的数值,为了解决这个问题,我们沿用之前的方法,使用线性插值。
如下图,2次查询各自层上通过双线性插值得到的结果,再通过1次线性插值,可得到最终结果,即三线性插值。
各向异性过滤(Anisotropic Filtering)
- 可以解决矩形(非正方形)的纹理区域覆盖
- 额外的开销是原本的3倍
EWA 过滤
- 使用多个查找
- 加权平均
- Mipmap 层次结构仍然有帮助
- 可以处理不规则的足迹
凹凸贴图
添加表面细节而不添加更多三角形
- 每个像素扰动表面法线(仅用于着色计算)
- 由纹理定义的每个纹素的“高度偏移”
- 通过凹凸贴图,改变相对高度,改变法线
如何改变法线
二维
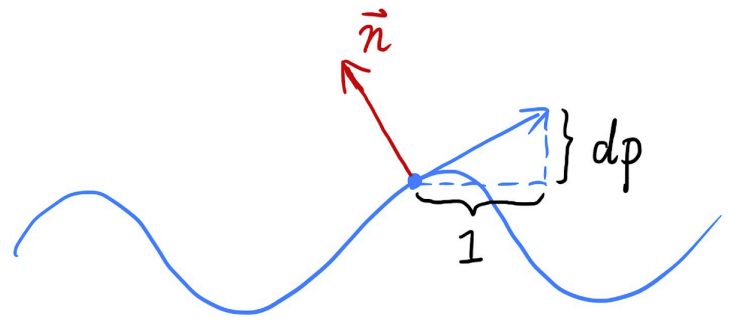
- 如下图所示,原本该点p的法线是n(p) = (0, 1)
- 引入凹凸贴图后,点p的变化量\(dp = c*[h(p+1)-h(p)]\),c是常数,表示凹凸贴图的影响,因此点p的切线可以表示为(1, dp)
- 法线与切线垂直,因此可以得到法线为\(n(p) = (-dp, 1).normalized()\)
三维
- 原本该点p的法线是n(p) = (0, 0, 1)
- p点切线\(\frac{dp}{du}=c1 * [h(u+1)-h(u)]\)和\(\frac{dp}{du}=c2*[h(v+1)-h(v)]\)
- 法线为\(n(p) = (-\frac{dp}{du}, -\frac{dp}{dv}, 1).normalized()\)
注意
这些是在局部坐标中的,之后还需要重新计算到世界坐标中。
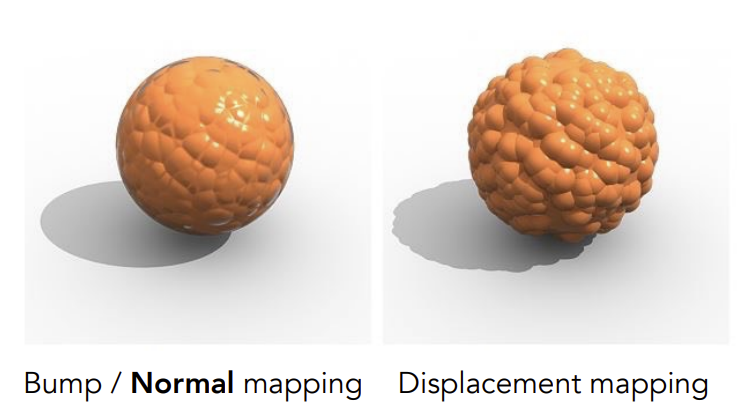
位移贴图——一种更高级的方法
- 与凹凸贴图一样的输入,一样的纹理
- 与凹凸贴图不一样,它会做位置的移动,实际上移动了顶点的位置
- 如下图所示,凹凸贴图下图形本身凹凸位置的阴影不够真实,影子也不够真实,是欺骗人视觉的效果,而非真实的点坐标
- 要求模型的三角形足够细、多
Shadow Mapping
一种图像空间算法
- 在阴影计算期间不了解场景的几何形状
- 必须处理混叠伪影
关键思想:
- 不在阴影中的点必须被光线和相机都看到
流程
- 从光源看向场景,相当于把摄像机放在光源,对准场景,做一遍光栅化
- 但是我们不对其做着色,而是记录看到的点的深度
- 将摄像机放在眼睛位置,真正地看向场景,记录看到的点的深度
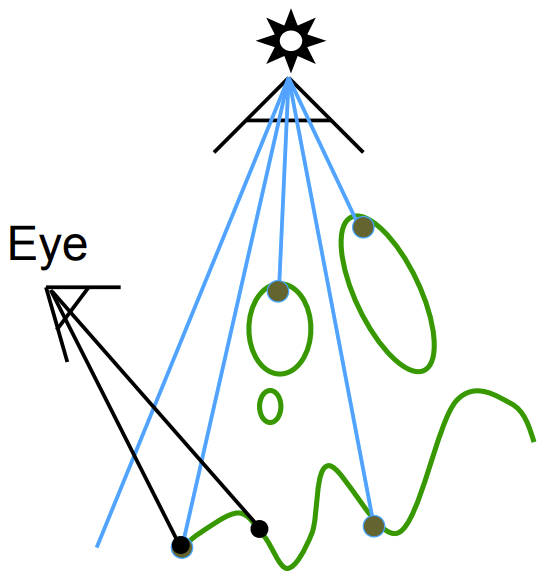
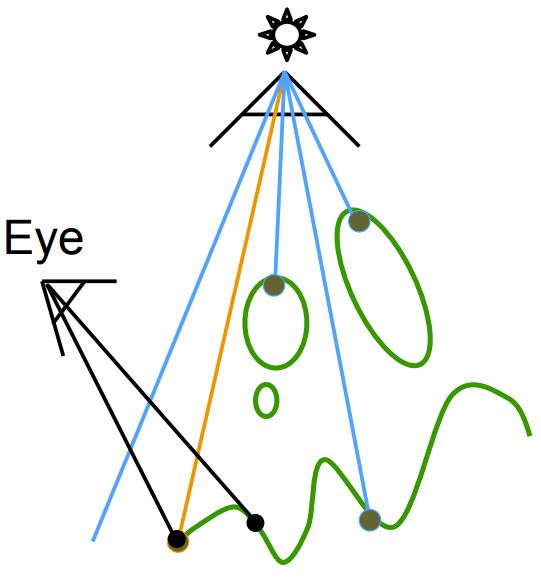
- 可以将看到的点投影回之前摄像机放在光源的虚拟成像上,如果我们从光源看这个点,它应该出现在图像的哪个位置上。从摄像机看这个点,这个点投影回光源,就知道它在之前深度图的哪个像素上。我们之前记录了该点的深度,此时可以计算该点到光源的深度,如果两个深度一致,说明该点是可以被光源看到的。该点是可见 的,可以被摄像机看到,也可以被光源看到。(如图3橙色线段所示)
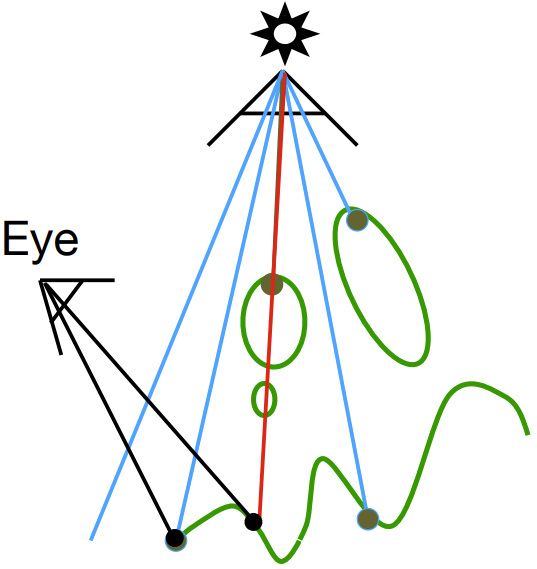
- 如果两者深度不一样,说明该点是之前光源看不到的点,说明该点在阴影中。(如图4红色线段所示)
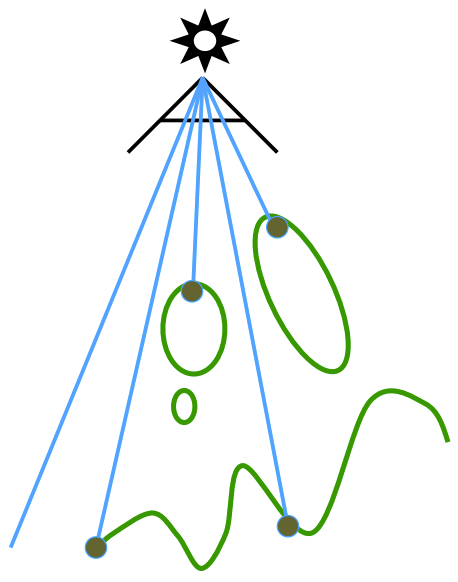
可视化Shadow Mapping过程
- 如下图所示,一个较为复杂带有阴影的场景,点光源在左上角
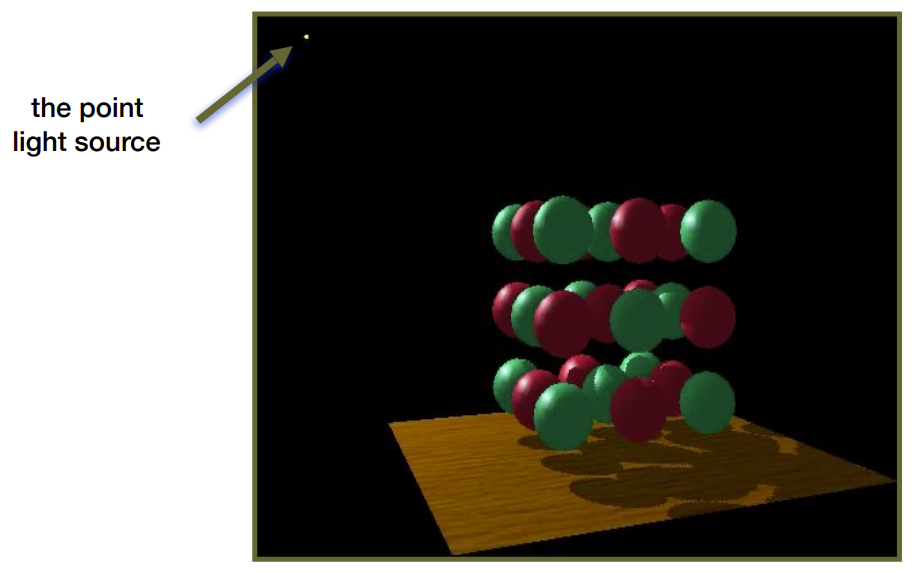
- 将摄像机放在光源位置,记录深度值
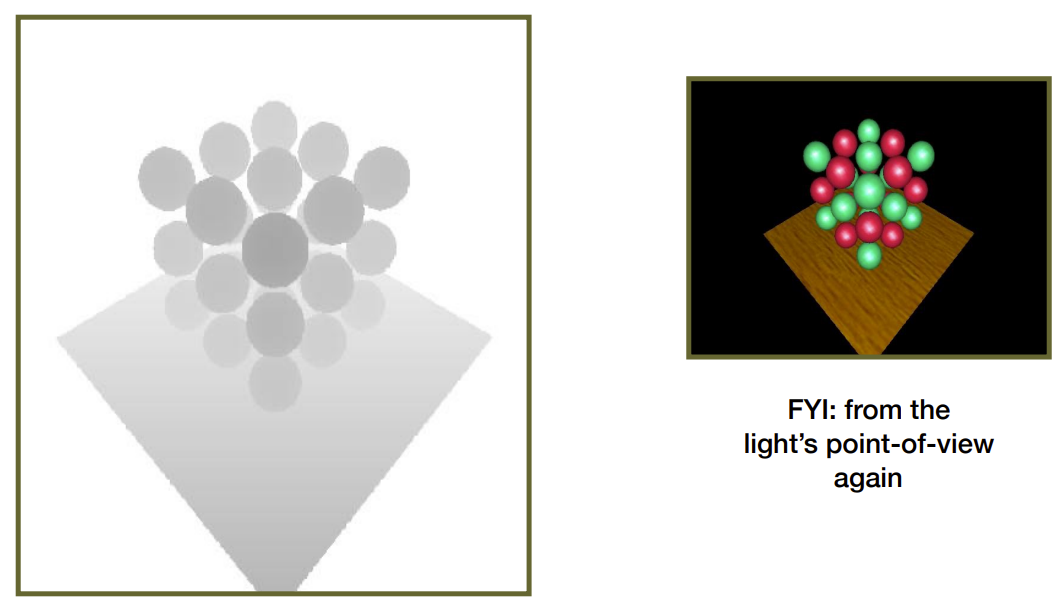
- 将摄像机摆在实际位置,绿色是阴影贴图上距离(光,shadow point)≈ 深度的地方,非绿色是阴影应该在的地方
- 但下图,球的上半区域存在灰色,可能是由于浮点判断误差引起的

存在的问题
- 硬阴影(仅限点光源)
- 质量取决于阴影贴图分辨率(基于图像的技术的一般问题)
- 涉及浮点深度值的相等比较意味着规模、偏差、容差问题
硬阴影与软阴影:
- 硬阴影是非0即1,没有过渡
- 软阴影有过渡,阴影是逐渐消失的
- 点光源不会产生软阴影,产生软阴影说明光源存在一定的大小
