Games101-Lecture13-16(Ray Tracing)学习笔记
本章内容
在之前的章节,我们已经学习了光栅化和几何部分,本章将讲述Ray Tracing(光线追踪)。
前言
为什么要光线追踪
光栅化不能很好地处理全局的效果:
- 软阴影
- 对于类似打磨比较光滑的金属、毛玻璃,有反射的高光,也有本身的粗糙性,光线会在场景中多次反射,光栅化的效果不是很好
光线追踪是准确的算法,但是非常慢:
- 光栅化是实时的,光线追踪是离线的
关于光线的3个想法
- 光以直线传播(虽然这是错误的)
- 光线交叉时不会相互“碰撞”(尽管这仍然是错误的)
- 光线从光源传播到眼睛(但物理在路径反转 - 互易性下是不变的)。
“如果你凝视深渊,深渊也会凝视你。” ——弗里德里希·威廉·尼采(翻译)
思想
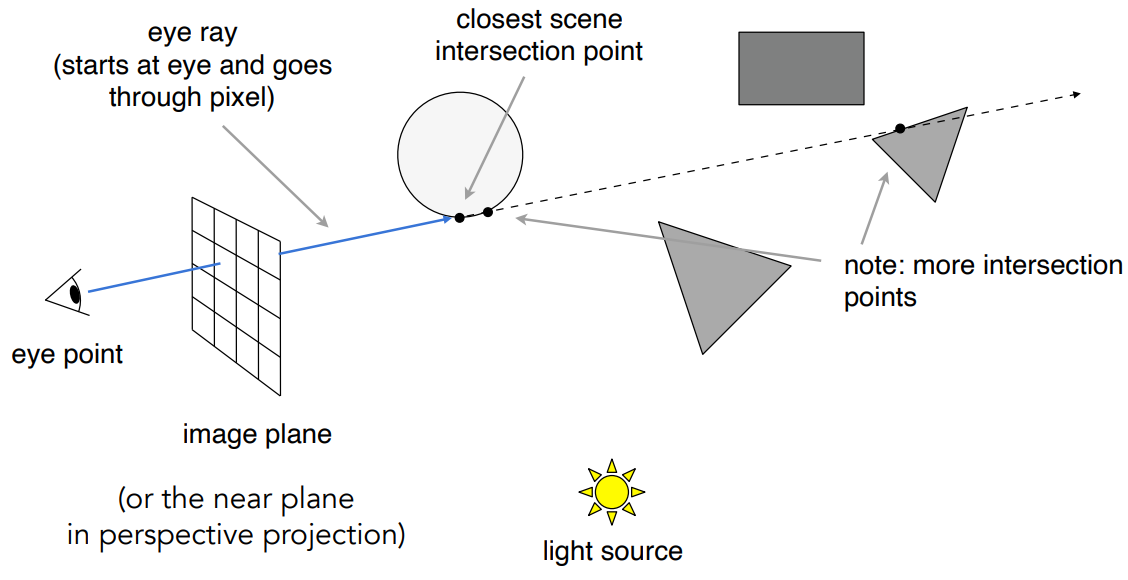
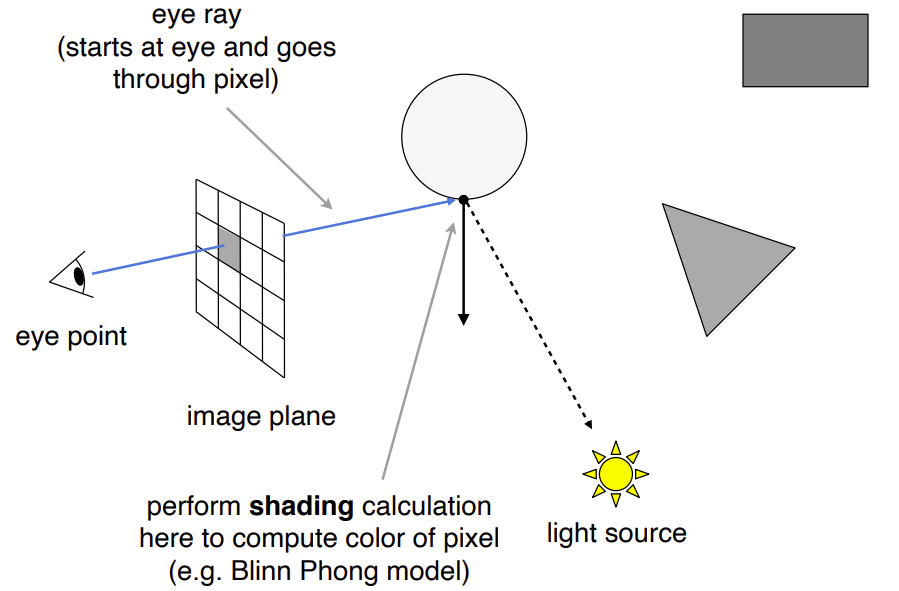
- 从人眼向屏幕的各个像素点发射一条光线,会打到场景中最近的物体(同时也解决了深度缓存问题)
- 如何判断该点是否被照亮呢?从该点向光源连接一条线(shadow ray),如果这条连线中不存在物体遮挡,则说明光源可以照亮整个点,否则在阴影中
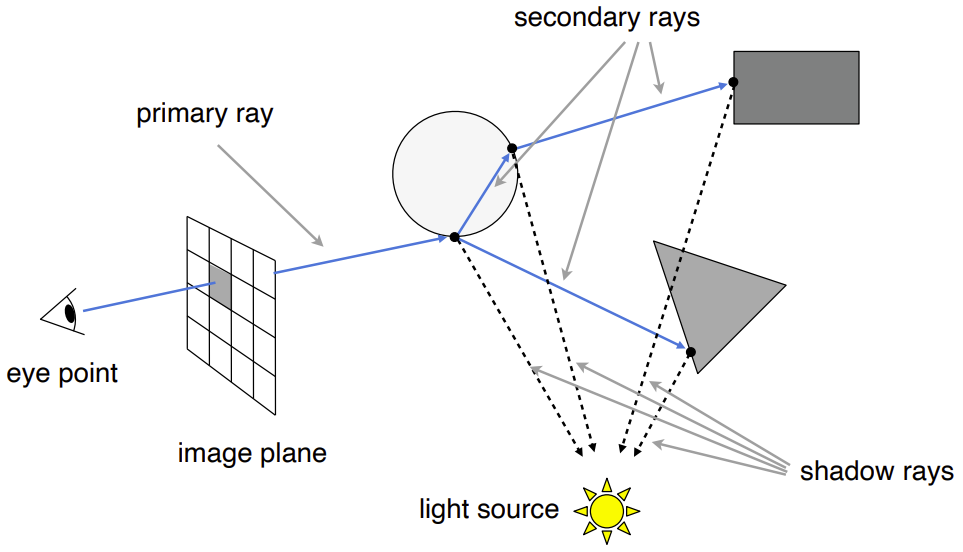
Whitted风格的光线追踪(递归)
实际上,一条光线可能经过多次折射、反射到多个点上,最终该像素的值是多个点累加的,折射、反射中存在能量损失。
光线求交
光线与面求交点
光线的定义:光源+一个方向向量,如下公式,从o开始,往d方向走了t的时间
\(r(t) = o+td, 0<t<\infty\)
光线与球求交点
光线:\(r(t) = o+td, 0<t<\infty\)
球:\(p:(p-c)^2-R^2=0\)
同时满足上述两个式子的点即为交点,即解
\((o+td-c)^2-R^2=0\)
光线与隐式表面求交点
光线:\(r(t) = o+td, 0<t<\infty\)
隐式表面:\(p:f(p)=0\)
替换光线的方程:\(f(o+td) = 0\)
解的要求:实数(有物理意义)、正数(时间为正)
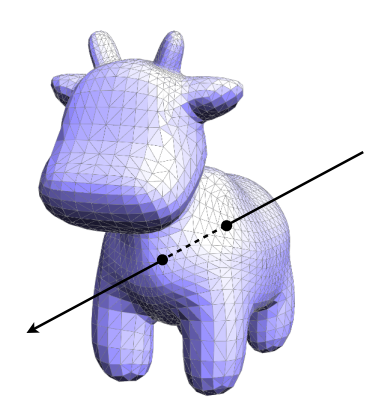
光线与三角网格求交点
作用
- 渲染:可视性、阴影、亮度
- 几何:是否在物体内,光线与物体有奇数个交点则光线在物体内,偶数个则在物体外(要求物体封闭没有洞)
思路
- 光线与每个三角形求交点
- 简单,但是很慢(考虑加速?)
- 光线与三角形有0个或者1个交点
光线与三角形求交点
思路
因为三角形在一个表面内,因此可以转换成如下两步判断:
- 光线与平面是否相交
- 交点是否在三角形内
平面可以由一个方向N和一个点p'定义,\(p:(p-p')*N=0\),N为法线。
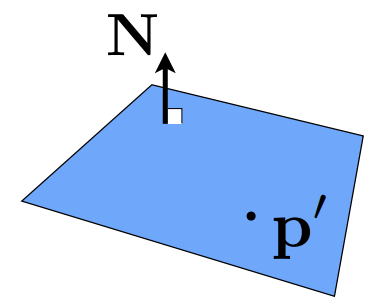
代入\(p=r(t)\)得,\((p-p')*N=(o+td-p')*N=0\)
Möller Trumbore算法
利用三角形的重心求解,联立可得
\(\vec{O}+t\vec{D}=(1-b_1-b_2)\vec{P_0}+b_1\vec{P_1}+b_2\vec{P_2}\)
再利用三维空间坐标求解即可。
加速光线与三角形求交点
包围盒
用一个包围盒将物体围住(包围盒不限形状),用简单的体积绑定复杂的对象
- 对象完全被包含在盒中
- 如果光线没有击中包围盒,光线必然不会击中对象
- 所以首先测试包围盒,然后测试对象是否击中物体

包围盒包含3个对面(上下、左右、前后),长方体就是3个对面形成的集合。
通常我们使用Axis-Aligned Bounding Box (AABB) (轴对齐包围盒),包围盒的每个面都与x轴或者y轴或者z轴平行。
光线与包围盒求交点
可以转换成光线与3个对面求交,知道光线进入的时间\(t_{min}\)和离开的时间\(t_{max}\),对于3组\(t_{min}\)和\(t_{max}\),它们的交集即为光线在包围盒内的时间区间。
- 光线只有在进入所有成对的平面时才进入包围盒
- 只要光线离开任何一对平面,光线就会离开包围盒
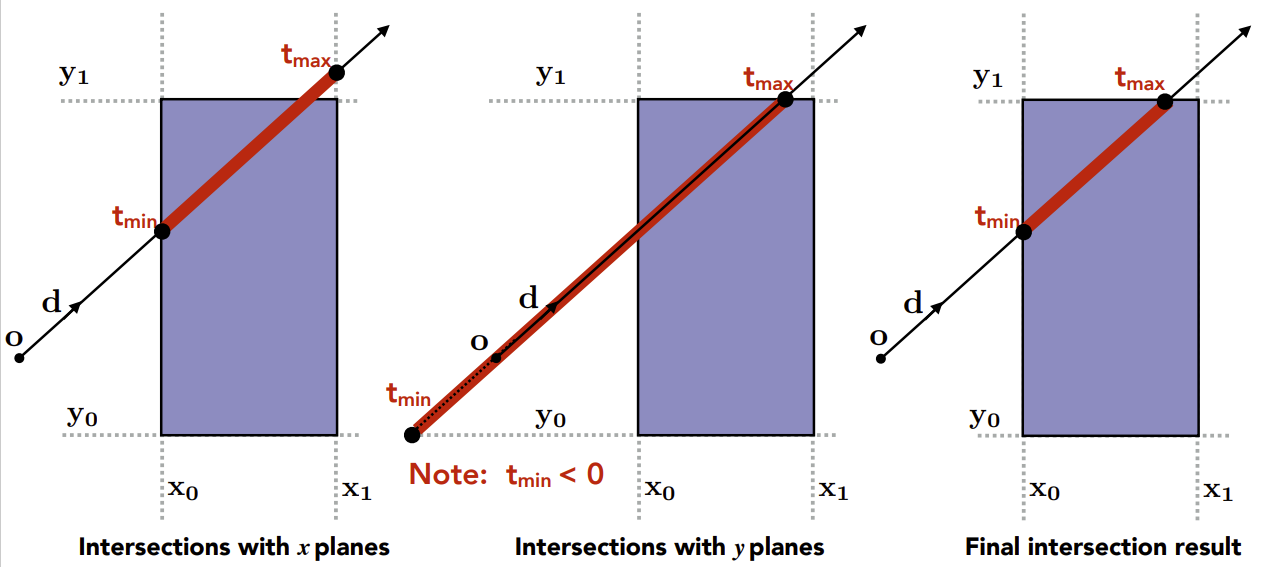
- 对于3D包围盒,\(t_{enter} = max(t_{min}), t_{exit} = min(t_{max})\)
- 如果\(t_{enter}<t_{exit}\),光线会在包围盒里呆一段时间。
- 如果\(t_{exit}<0\),包围盒在光线背面,没有交点
- 如果\(t_{enter}<0, t_{exit}\geq0\),光源在包围盒内,有交点
- 总之,光线与包围盒有交点,当且仅当\(t_{enter}<t_{exit}\) && \(t_{exit}\geq0\)
为什么包围盒选择轴对齐
可以简化计算过程,如下图所示。
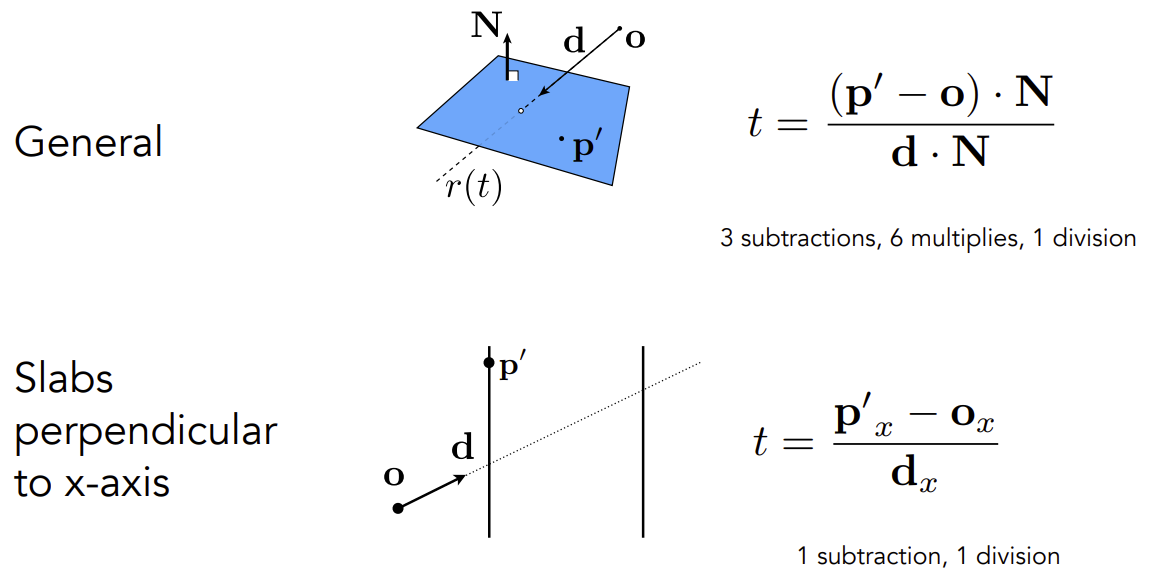
使用AABB加速光线追踪(Whitted风格的光线追踪)
- 规则的网格
- 空间划分
统一的空间划分(网格)
在光线追踪之前,进行的预操作
- 找到物体的包围盒
- 创建网格
- 标记可能有物体的格子(下图有误,右上角第二个格子也要涂黑)
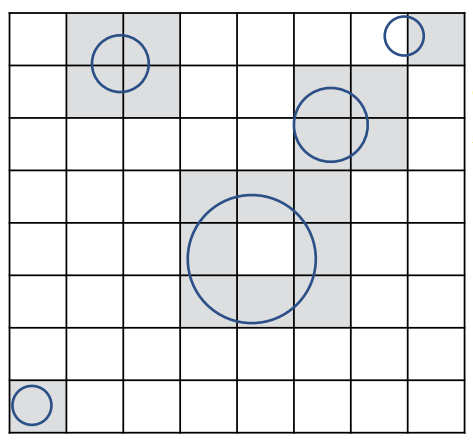
如下图所示,一条光线从左边射入,从右边打出,当我们将空间划分为这些均匀的格子区域后,相比于判断光线是否与物体相交,我们更易于判断光线是否与格子相交。
当光线与格子相交时,再判断光线是否与格子内的物体相交。可以避免光线与所有物体求交。
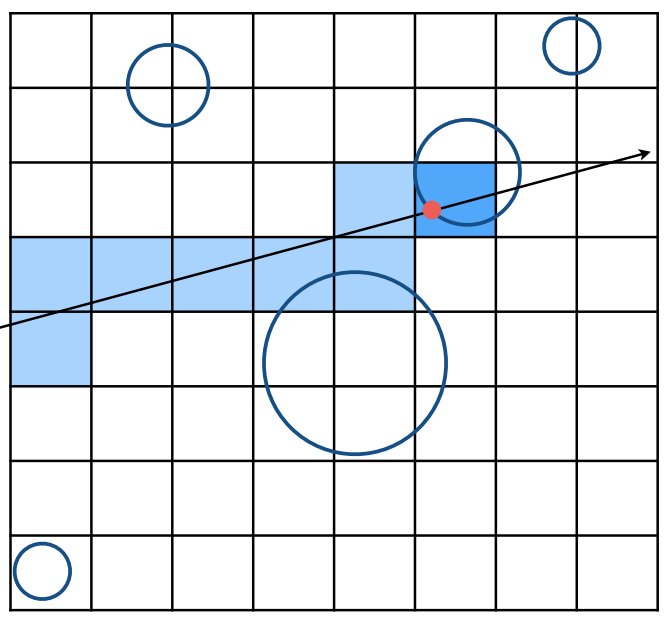
当格子划分太稀疏的时候,没有加速效果;当格子划分太密集的时候,判断光线与格子是否相交过多,会影响效率。所以格子划分的数量需要适中。
空间划分
空间划分示例
- 八叉树(Oct-Tree),每次从空间的每个维度划分空间。
- KD-Tree,每次只从空间的一个维度划分空间,比如x、y、z轴循环划分。
- BSP-Tree,每次选择一个方向进行划分,但可能是斜的。
KD-Tree预处理
如下图所示,每次按照不同的方向对空间进行划分,形成右边的树形结构。叶子节点存储和对应格子相交的几何形体。
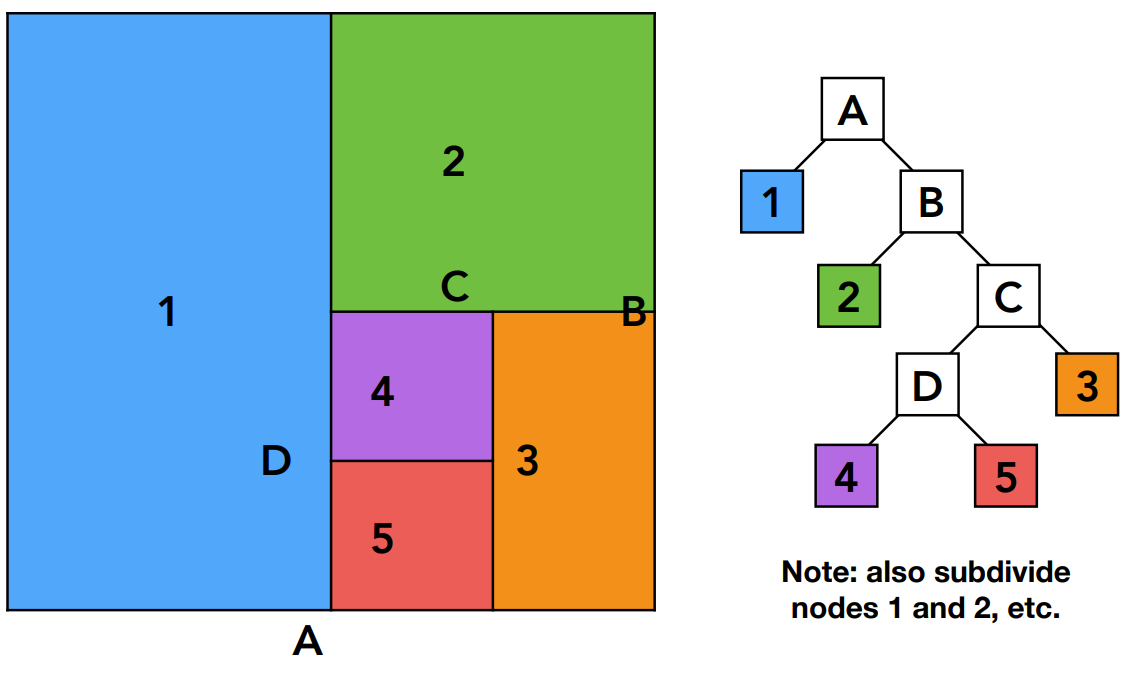
KD-Tree的数据结构
内部节点存储:
- 分割轴:x 轴、y 轴或 z 轴
- 分割位置:分割平面沿轴的坐标
- children:指向子节点的指针
- 没有对象存储在内部节点中
叶节点存储:
- 对应空间内的物体对象列表
- 一个物体可能出现在多个叶子节点上
遍历一个KD-Tree
如下图所示,该光线遍历KD-Tree后,判断与叶子节点相交,最终会经过1、2、3节点。当光线与节点有交点后,再去判断光线是否与对应空间内的物体相交。
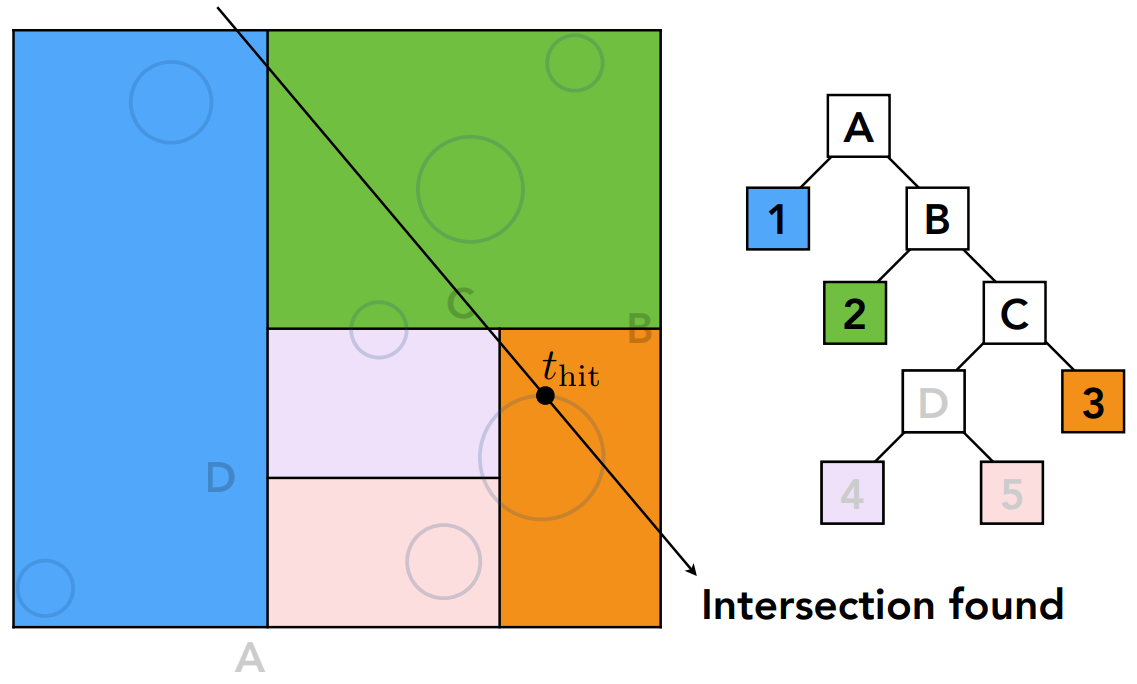
对象划分和Bounding Volume Hierarchy (BVH)
将物体分为两堆,并重新求物体的包围盒,同时满足物体只会出现在一个包围盒里,避免了之前一个物体会出现在多个包围盒里。BVH的包围盒是可能相交的。
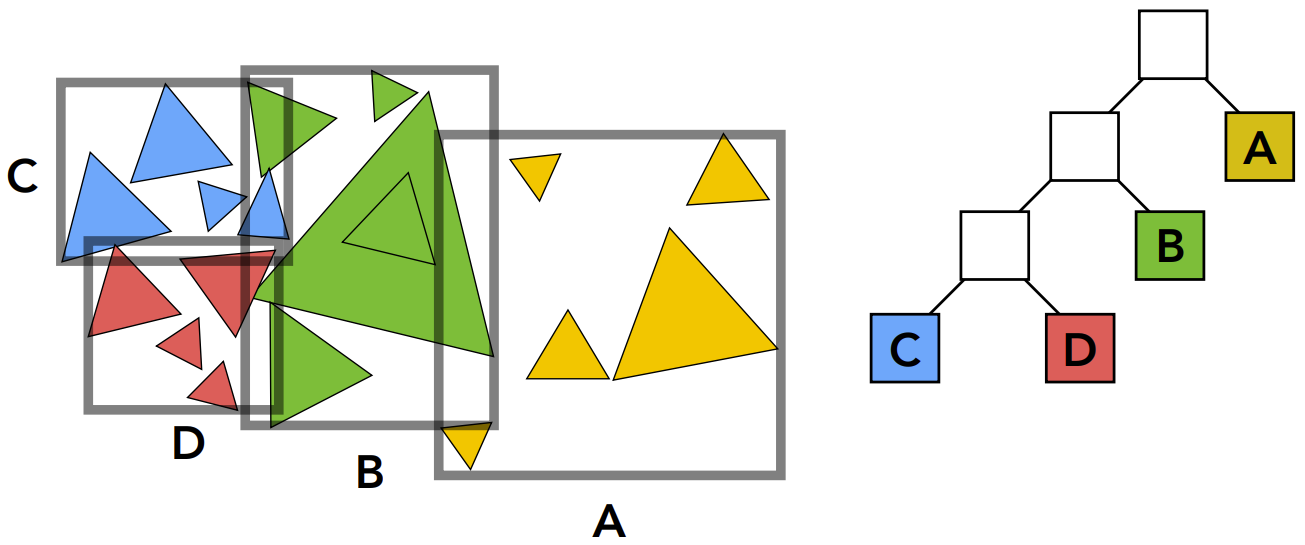
- 查找包围盒
- 递归地将对象集拆分为两个子集
- 重新计算子集的包围盒
- 必要时停止
- 在每个叶节点中存储对象
构建BVHs
如何细分节点:
- 选择要拆分的维度
- 启发式#1:始终选择节点中的最长轴
- 启发式#2:在中间对象位置拆分节点,可以使得树尽可能平衡
终止标准:
- 启发式:当节点包含少量元素时停止(例如 5 个)
BVH的数据结构
内部节点存储:
- 包围盒
- Children:指向子节点的指针
叶节点存储:
- 包围盒
- 对象列表
节点表示场景中的图元子集
- 子树中的所有对象
空间划分与对象划分
空间分区(例如 KD-tree): - 将空间划分为不重叠的区域 - 一个对象可以包含在多个区域中
对象分区(例如 BVH):
- 将对象集划分为不相交的子集
- 每个集合的边界框可能在空间上重叠
辐射度量学(Basic radiometry)
前言
之前在 Blinn-Phong 模型没有考虑能量的损失,辐射度量学相当于更高级的光线追踪,得到更准确的结果。
照明测量系统和单元
准确测量光的空间特性
新术语:Radiant flux、intensity、irradiance、radiance
将以物理上正确的方式执行照明计算
Radiant Energy and Flux (Power)
能量和功率(单位时间内收到的能量),图形学中常用的是单位时间内的能量。
Radiant Intensity
每个单位立体角(solid angle)上的能量。
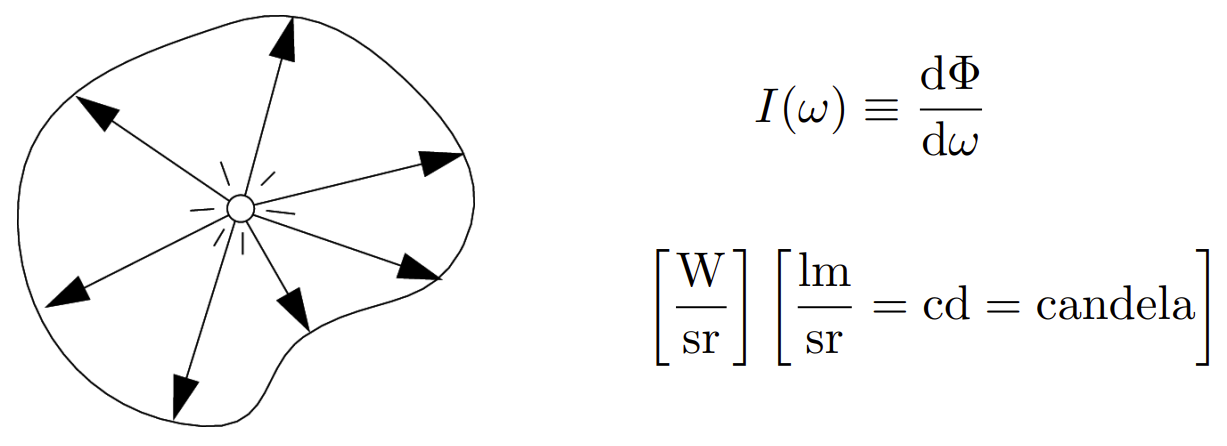
Angles and Solid Angles
弧度:圆上的对圆弧长度与半径之比
- \(\theta = \frac{l}{r}\)
- 圆有\(2\pi\)的弧度
立体角:球体对向面积与半径平方的比值
- \(\Omega=\frac{A}{r^2}\)
- 球有\(4\pi\)的弧度
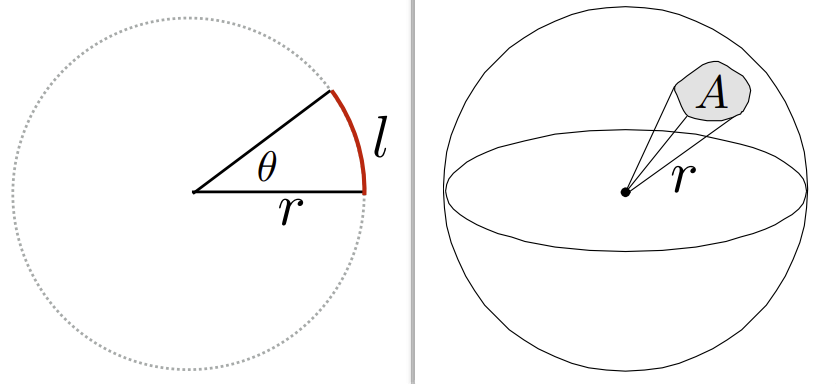
Differential Solid Angles(微分立体角)
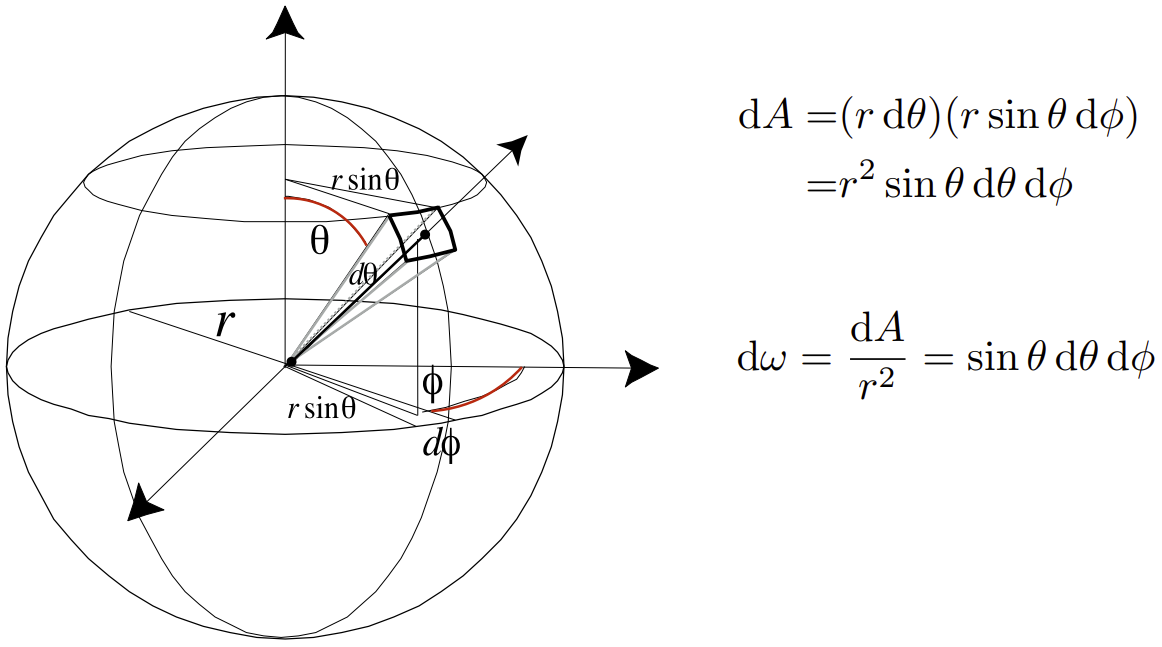
Isotropic Point Source
点光源
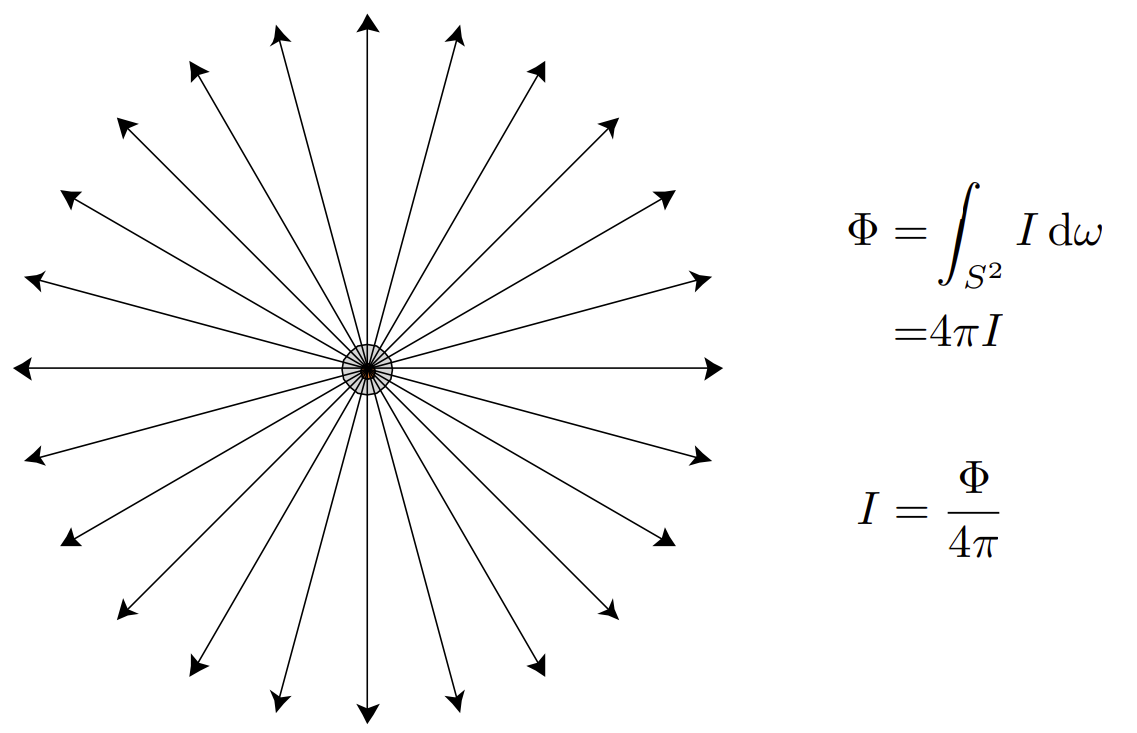
Irradiance
单位面积的功率,表面的Irradiance与光方向和表面法线之间夹角的余弦成正比。
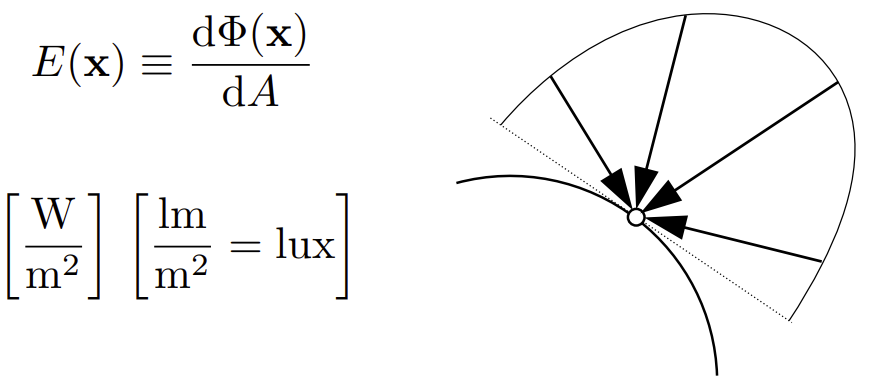
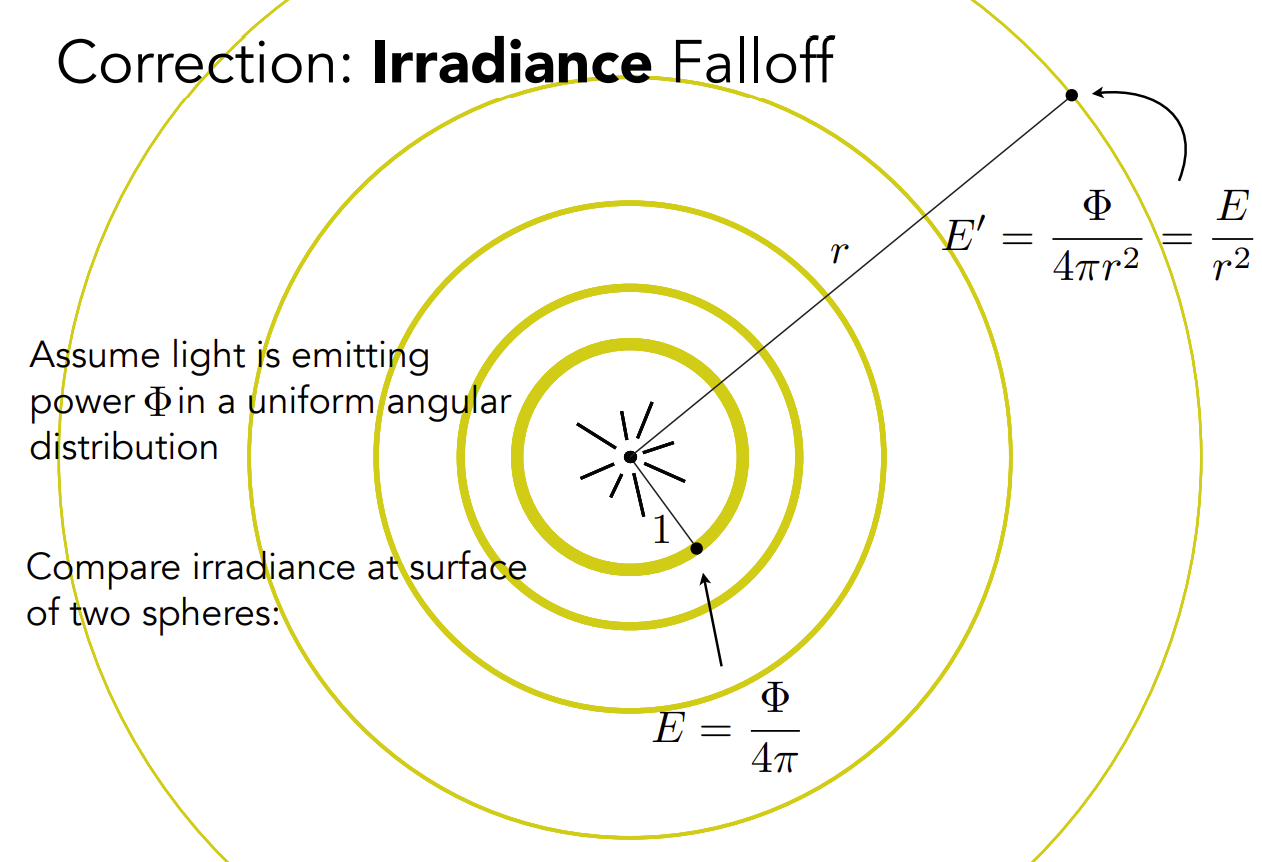
Irradiance Falloff
校正:辐照度衰减。
假设光以均匀的角度分布发射功率,比较两个球体表面的辐照度:
单位半径上,表面的Irradiance为\(E=\frac{\Phi}{4\pi}\),半径为r的表面Irradiance上,\(E'=\frac{\Phi}{4\pi{r^2}}\)
Radiance
辐射度(亮度)是每单位立体角和每单位投影面积上,由表面反射、发射或接收的能量,在特定方向上的能量。
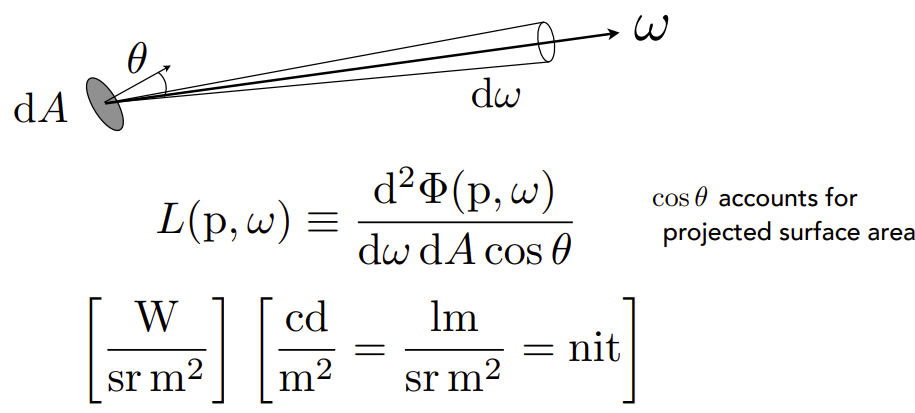
比较
- Irradiance: power per projected unit area
- Intensity: power per solid angle
- Radiance: Irradiance per solid angle
- Radiance: Intensity per projected unit area
Incident Radiance

Exiting Radiance

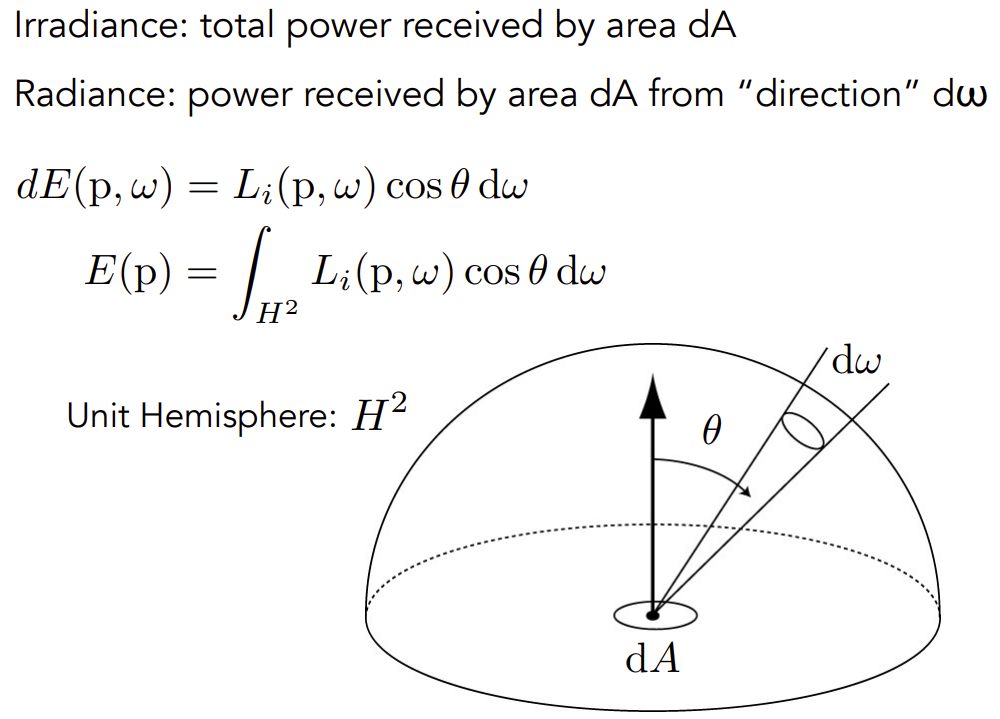
Irradiance和Radiance
Irradiance:在某个dA的微表面上,收到的所有能量。
Radiance:在某个dA的微表面上,从某个方向收到的所有能量。
Bidirectional Reflectance Distribution Function (BRDF)和Reflection Equation(反射方程)
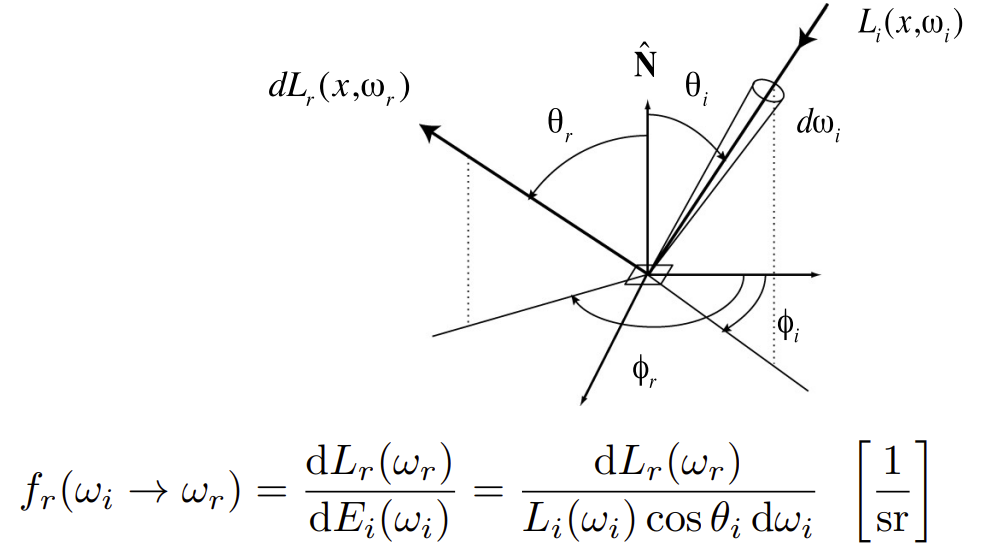
dA的微表面接收到的Irradiance可以计算出来,接着会辐射到各个方向都有,BRDF的定义就是如何对其在不同方向上的分配。
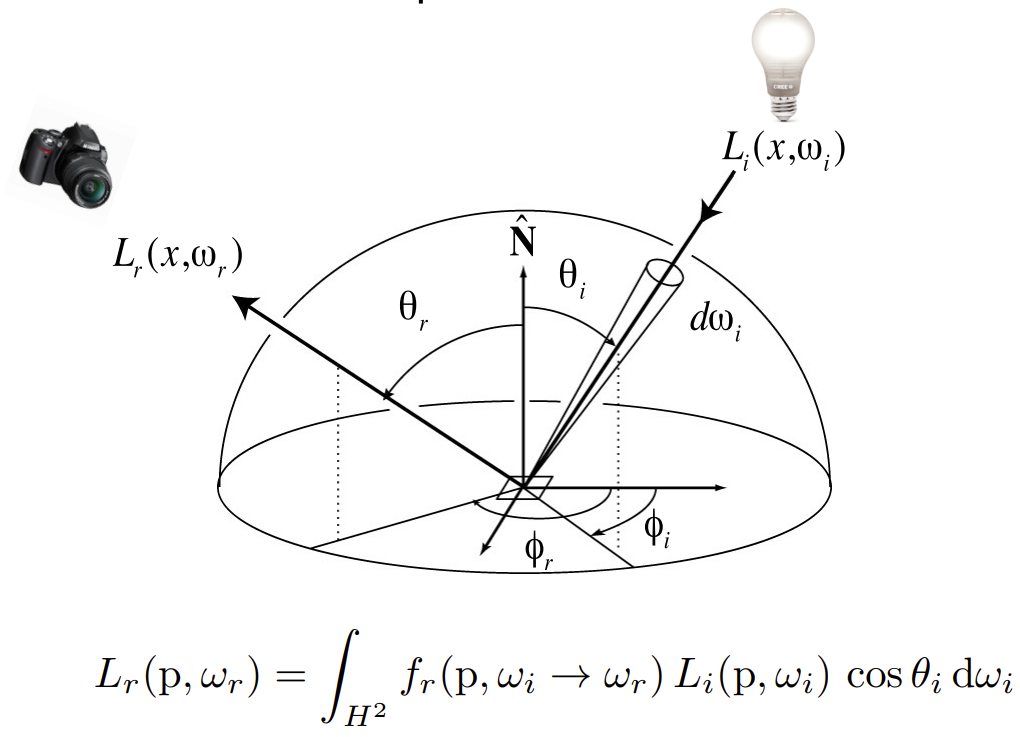
BRDF 相当于决定了物体的材质,告诉我们从某一个方向上考虑光线的入射,它从某一个方向反射的结果。通过对所有入射方向光线的累计,可以得到最终出射方向的光线,如下图2的反射方程所示。
同时,入射光线不一定只来自光源,可能是光源打到别的物体上的反射造成的,是一个递归问题。
Rendering Equation(渲染方程)
Reflection Equation如下
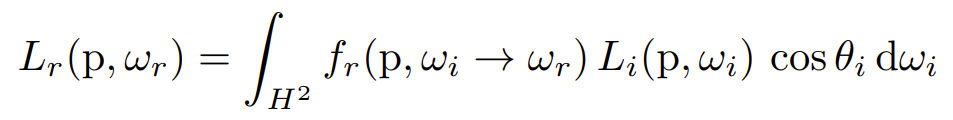
Rendering Equation如下,物体往某个方向出射的光包含两部分:自己产生发射的、其它入射的Radiance经过BRDF产生的。
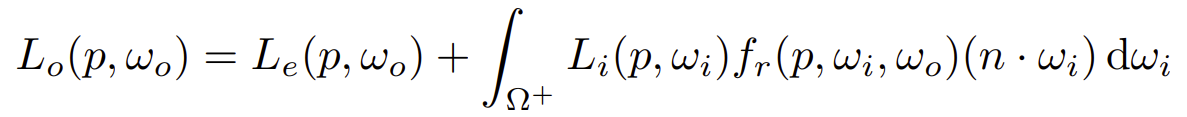
Reflection Equation 和 Rendering Equation
Reflection Equation
反射方程如下,包含自身的发出的光 + 从光源打到该点经由 BRDF 在特定角度的光。
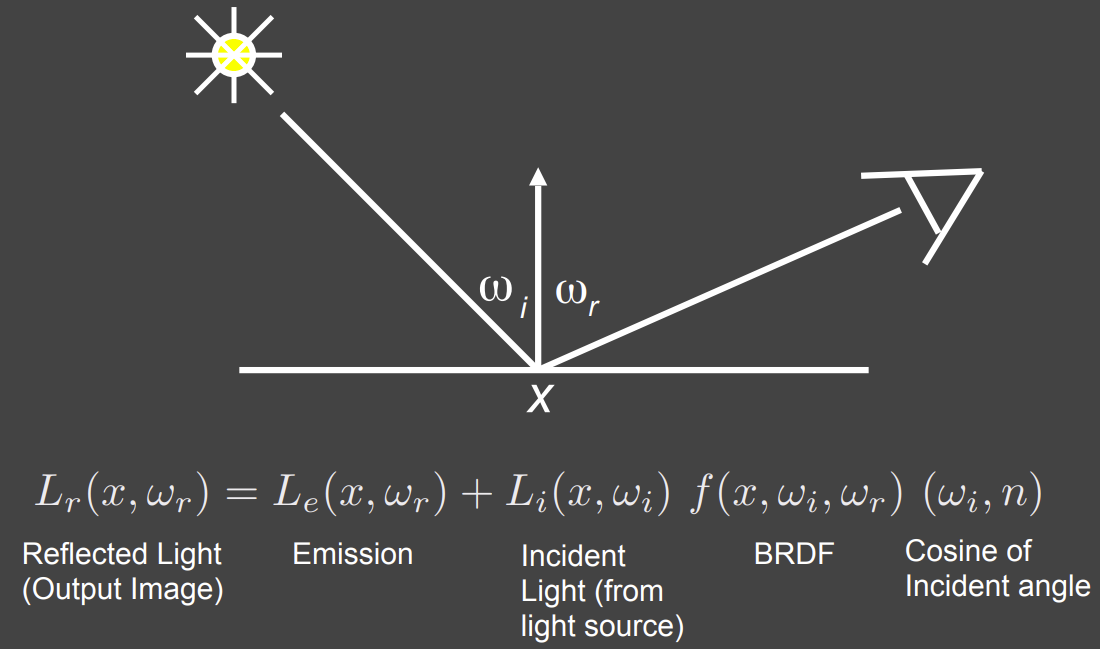
如下图所示,如果有多个点光源,我们则需要将点光源打到该点产生的反射进行累加。
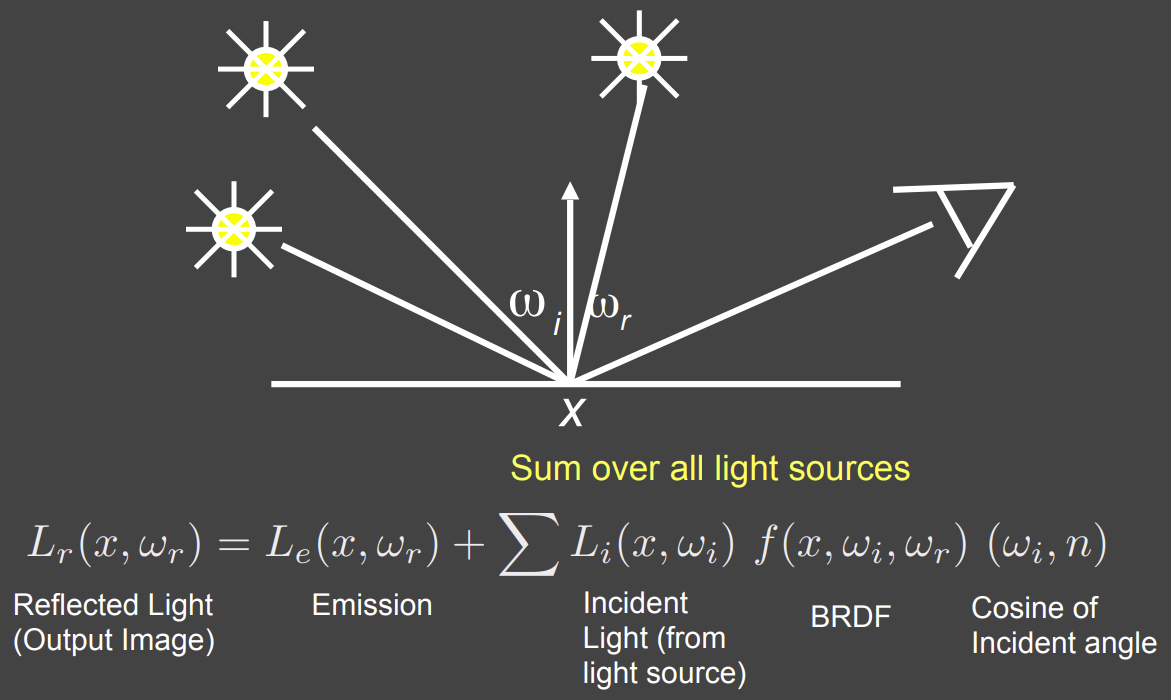
如下图所示,如果存在面光源,面光源可以看作是点光源的集合,我们则需要对面光源求积分。
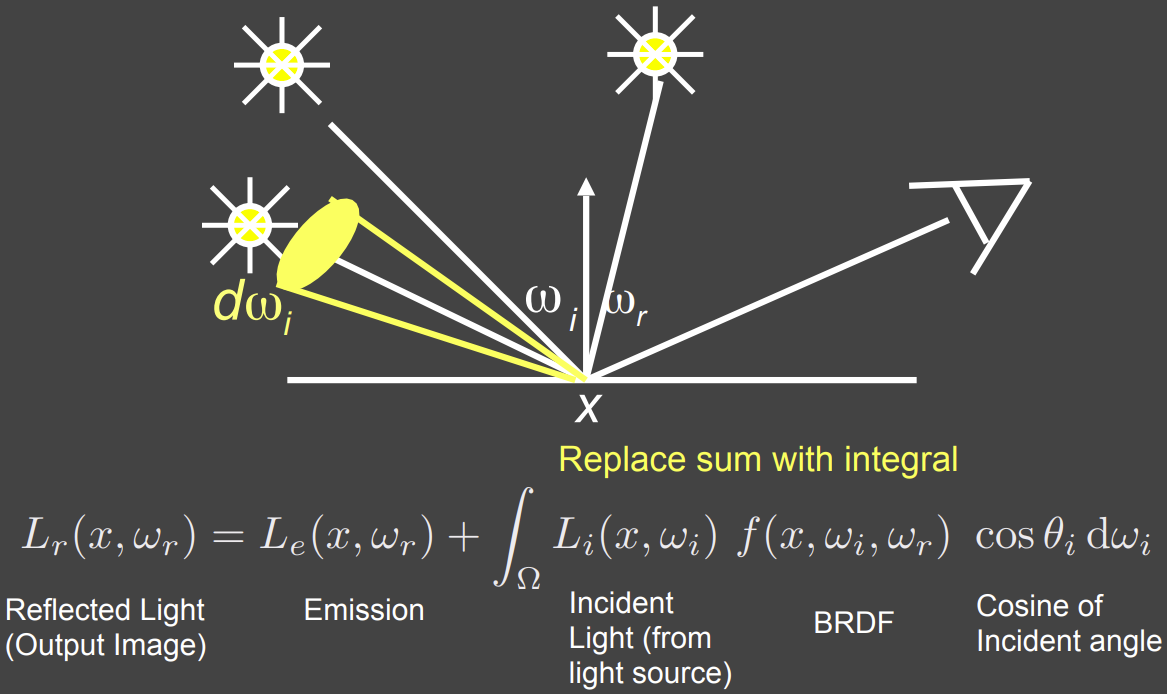
Rendering Equation
如果是由其它物体反射或者发出的光线,我们可以同样视其为光源,同时对于本渲染方程的求解可以看作是一个递归问题。
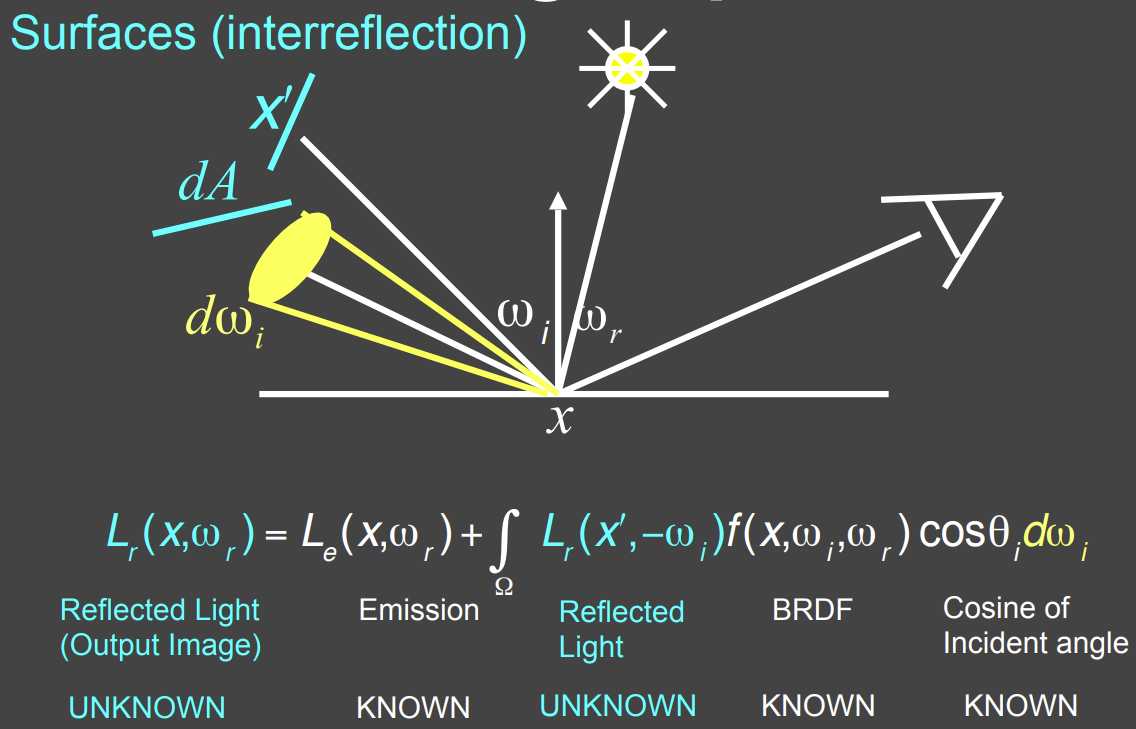
Rendering Equation可以通过数学简写,写成下图的积分方程形式。

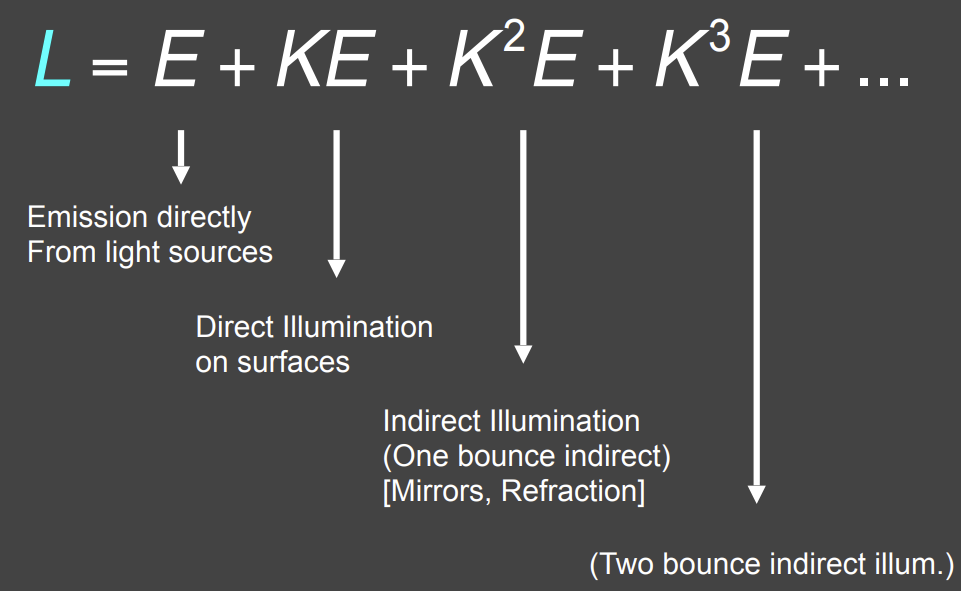
最终可写成下图数学形式,再通过类似泰勒展开的形式,将\((I-K)^{-1}\)展开成\((I+K+K^2+K^3+...)\),进而可以得到图3,相当于我们可以把最终看到的能量,直接看到光源的结果 + 光源辐射的能量经过1次反射后的结果 + 光源辐射的能量经过2次反射后的结果 + ... + 光源辐射的能量经过多次反射后的结果。
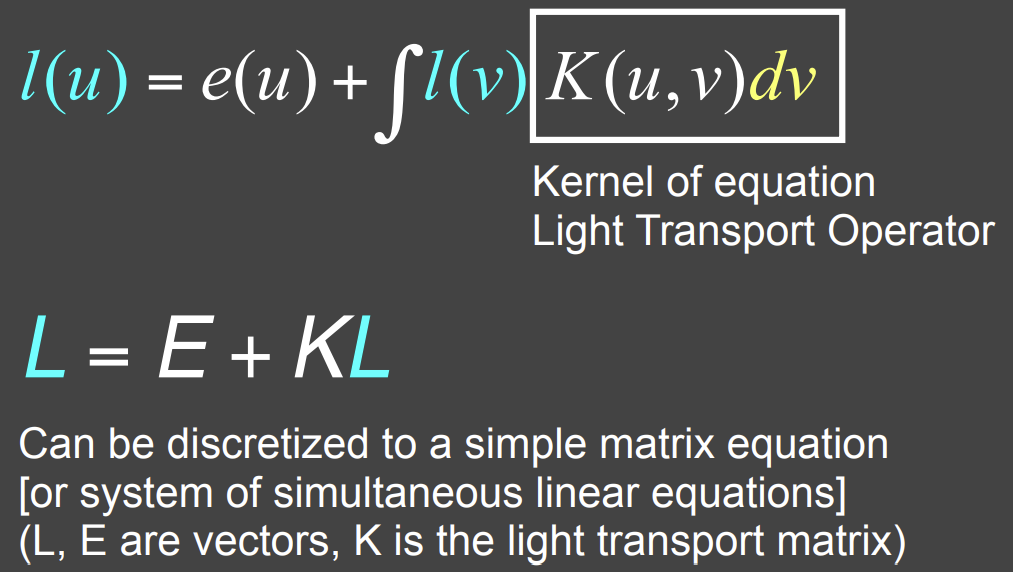

因此,对于全局光照的理解,全局光照 ≠ 间接光照,而是等于直接光照和间接光照的集合。
之前学习的光栅化操作,等于0次反射(光源本身)和1次反射(直接光照),即下图的\(E+KE\)部分。
Monte Carlo Integration(蒙特卡洛积分)
Why
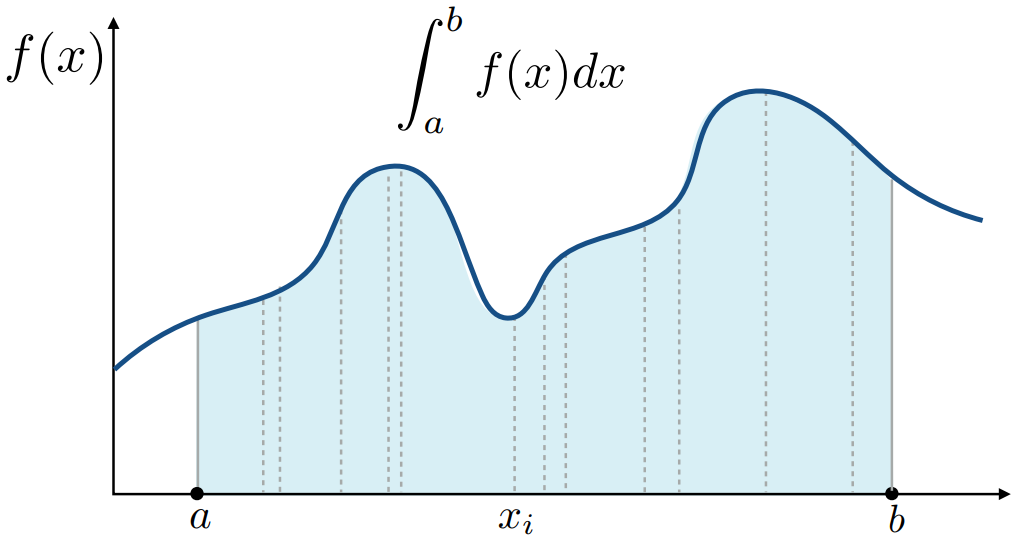
求一个函数的定积分,但解析求解比较复杂
What & How
通过平均函数值的随机样本来估计函数的积分。相当于在积分域内不断采样,采样的x有对应的y值,将积分的图形视作长方形(长为积分域,宽为y),求得面积,最后把所有长方形面积相加求平均。
近似方法
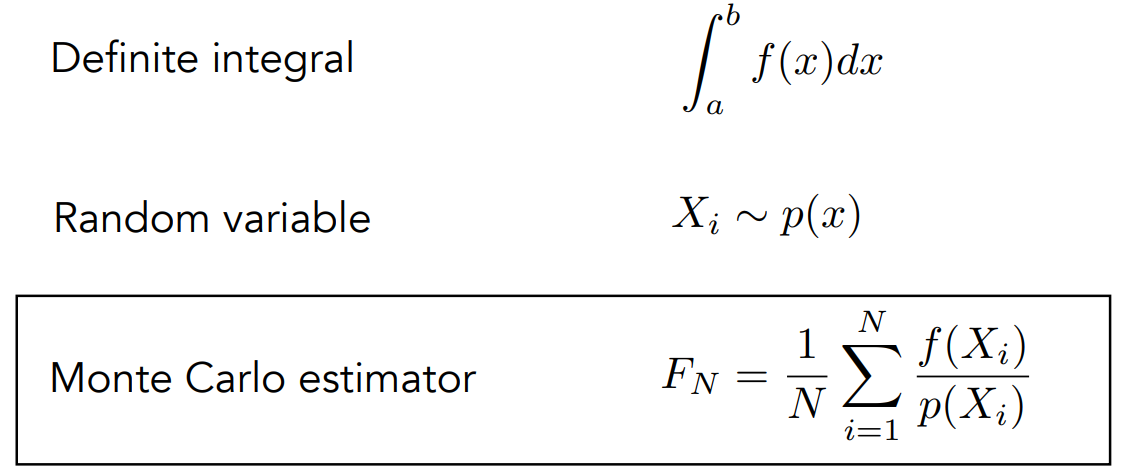
 \[
\int{f(x)} dx = \frac{1}{N}\sum_{i=1}^{N}\frac{f(X_i)}{p(X_i)} \quad ,
\quad X_i\sim p(x)
\]
\[
\int{f(x)} dx = \frac{1}{N}\sum_{i=1}^{N}\frac{f(X_i)}{p(X_i)} \quad ,
\quad X_i\sim p(x)
\]
- 样本越多,方差越小,近似值越高
- 在 x 上采样,在 x 上积分
Path Tracing(路径追踪)
前言
Whitted-Style Ray Tracing:
- 始终执行镜面反射/折射
- 停止在漫反射表面弹跳,如果光线打到漫反射的物体,光线就停止了,不再继续走了
Whitted-Style Ray Tracing的问题
- 对于Glossy材质的镜面反射不够真实

- 漫反射材质之间没有反射

求解Rendering Equation
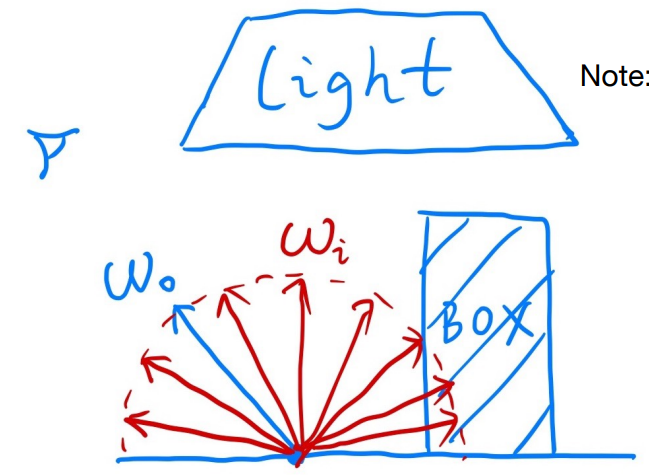
如下图所示,图的上方是光源,摄像机在左上角,我们想要观测的点在下方中间位置,通过蒙特卡洛积分,求解Rendering Equation,因为散发的光呈半球,所以蒙特卡洛积分的\(p(X_k)=\frac{1}{2\pi}\)(假设均匀采样半球,半球面的表面积为\(2\pi\))
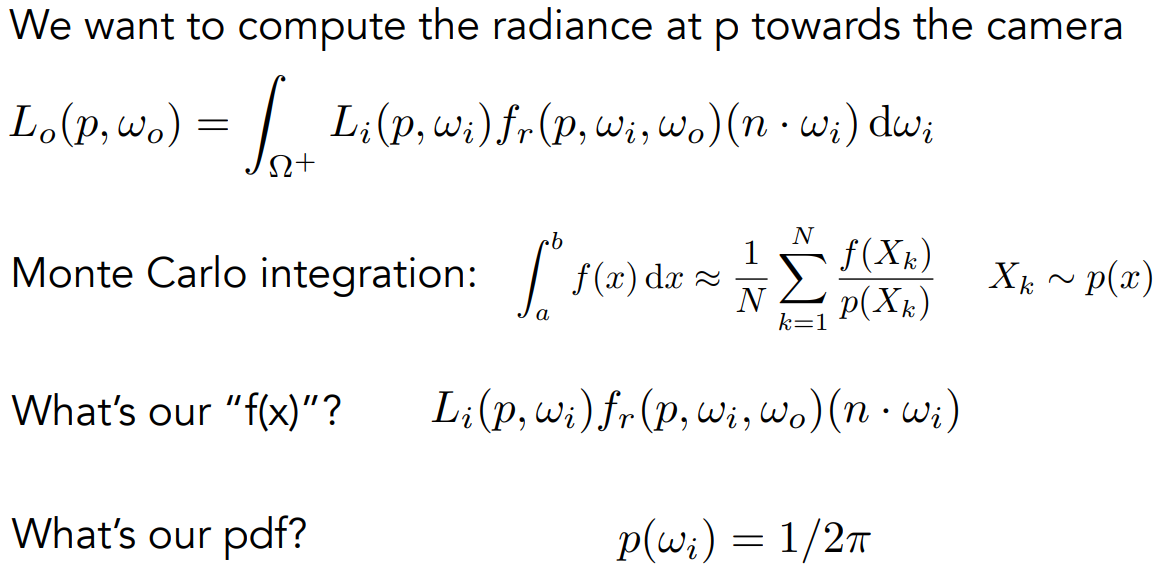
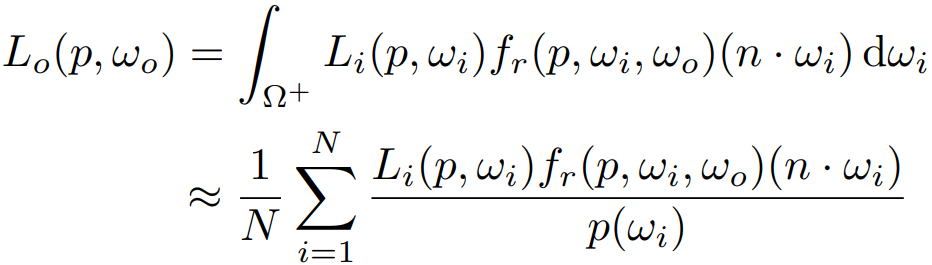
伪代码

引入全局光照
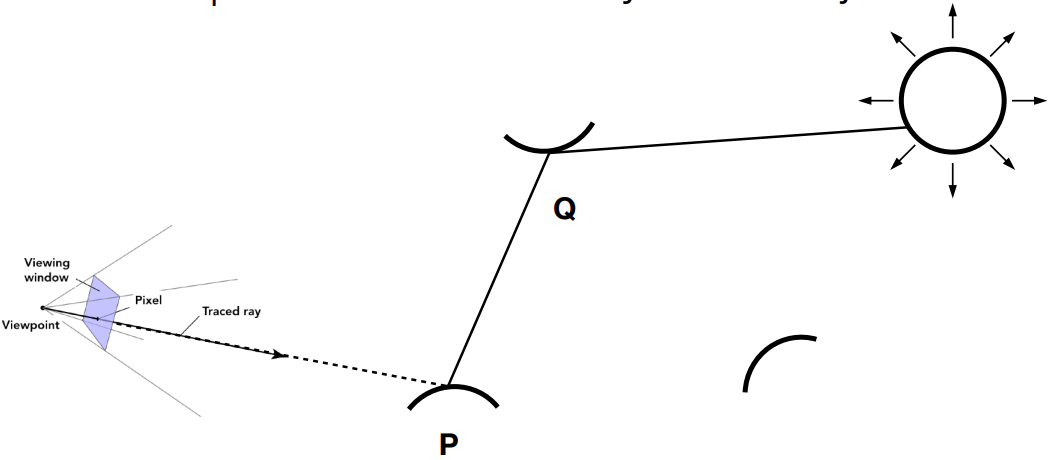
如果摄像机打到第一个物体反射的光线没有打到光源,而是打到了第二个物体(面光源),我们该如何计算?
我们可以进行递归操作,将第一个物体视作摄像机,第二个物体视作第一个物体,递归代入之前的函数中,判断光线从第二个物体反射后是否会打到光源,伪代码如下。

光线的数量会爆炸
第一个物体反射100个光线,到第二个物体100个光线再变成10000个光线,\(rays=N^{bounces}\),为了避免光线数量爆炸,我们可以设置每个着色点只打出一根光线,改写如下,为了降噪,需要打出多条光线进行追踪

递归停止的条件
在之前的操作中,我们总是在一个着色点上射一条射线,得到着色结果 \(Lo\)
类似俄罗斯轮盘赌的思想,假设我们手动设置一个概率 P (0 < P <
1),以概率P,射出一条射线,返回着色结果除以P:\(Lo/P\),以概率为
1-P,不发射光线,得到着色结果 0
这样,可以得到期望 Lo,\(E=P*(Lo/P)+(1-P)*0=Lo\)

效率低
我们现在已经有了Path Tracing的正确流程,但实际上可能效率并不高,如下图所示,从1至3,打到光源需要的光线数量在依次增加,原因是着色点在均匀地往四面八方打出光线采样,实际上有相当的光线被浪费了。
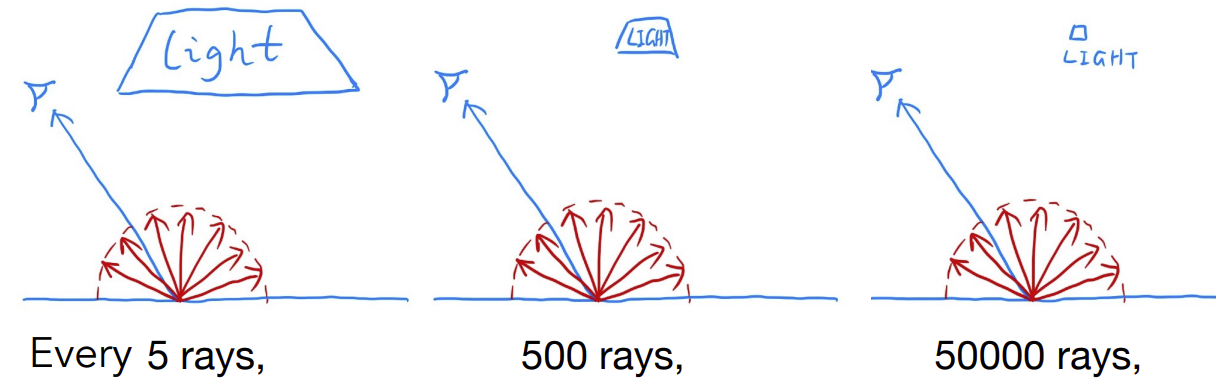
采样光源
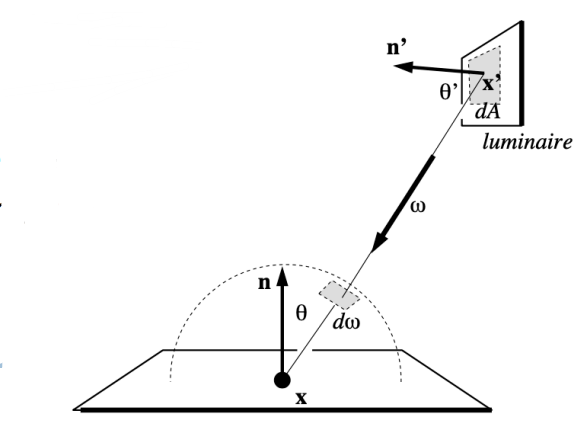
将光源与着色点相连,可以得到光源上的立体角与着色点上立体角的关系,代入可得(相当于改变积分域)
\[
dw=\frac{dA\cos\theta'}{||x'-x||^2}
\]
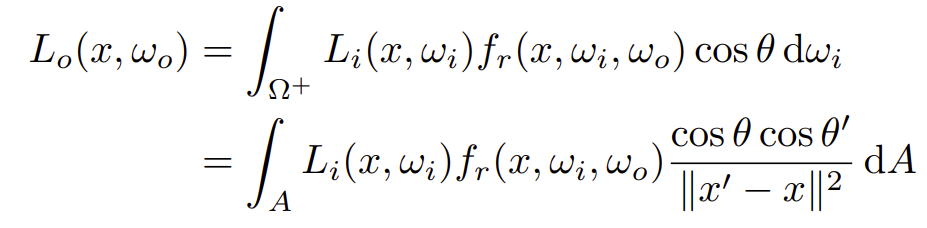
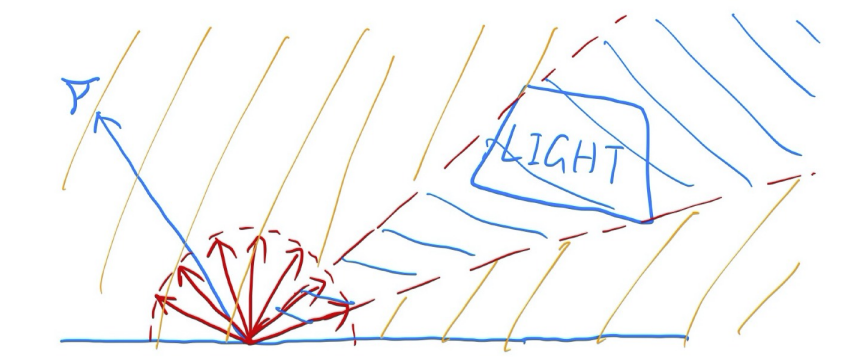
以前,我们假设光线是由均匀半球采样“意外”拍摄的,现在我们考虑来自两个部分的辐射,如下图所示:
- 光源(直接,下图右边区域,无需俄罗斯轮盘赌)
- 其他反射物体(间接,下图左边区域,应用俄罗斯轮盘赌)
伪代码如下:

判断采样点与光源的路线上是否被遮挡:
