LeetCode-6032 得到要求路径的最小带权子图

发表于 分类于 本文字数： 2.2k 阅读时长 ≈ 2 分钟

本章内容

本章为LeetCode-2203. 得到要求路径的最小带权子图的题解。

题目内容

给你一个整数 n ，它表示一个 带权有向图 的节点数，节点编号为 0 到 n - 1 。

同时给你一个二维整数数组 edges ，其中 \(edges[i] = [from_i, to_i, weight_i]\) ，表示从 \(from_i\) 到 \(to_i\) 有一条边权为 \(weight_i\) 的 有向 边。

最后，给你三个 互不相同 的整数src1 ，src2 和 dest ，表示图中三个不同的点。

请你从图中选出一个 边权和最小 的子图，使得从 src1 和 src2 出发，在这个子图中，都 可以 到达 dest 。如果这样的子图不存在，请返回 -1 。

子图 中的点和边都应该属于原图的一部分。子图的边权和定义为它所包含的所有边的权值之和。

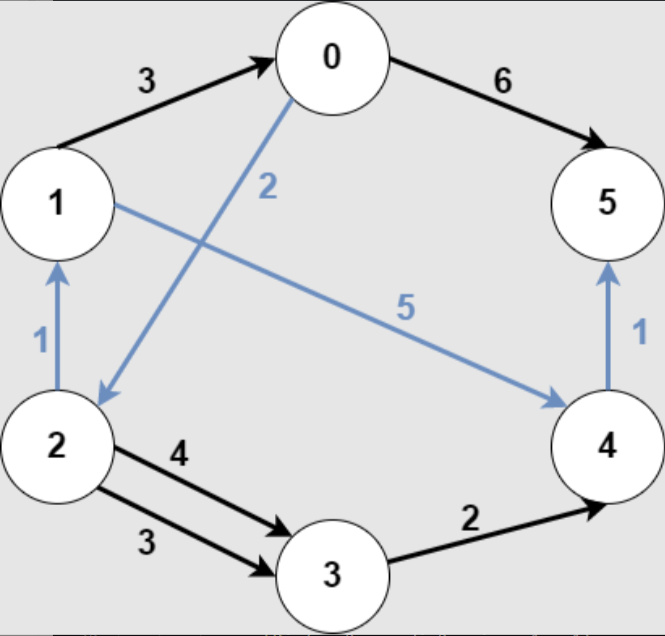
输入：n = 6, edges = [[0,2,2], [0,5,6], [1,0,3], [1,4,5], [2,1,1], [2,3,3], [2,3,4], [3,4,2], [4,5,1]], src1 = 0, src2 = 1, dest = 5 输出：9

解释：

上图为输入的图。

蓝色边为最优子图之一。

注意，子图 [[1,0,3], [0,5,6]] 也能得到最优解，但无法在满足所有限制的前提下，得到更优解。

解题思路

做LeetCode比赛的时候遇到这题，刚看见的时候感觉应该不难，但因为没有时间就没能深入思考。

实际上本题不难，用的也是图论中比较经典的思想，枚举中间点，通过枚举中间点\(i\)，计算src1到\(i\)的距离 + src2到\(i\)的距离 + \(i\)到dest的距离，求出最小的\(i\)，上述的枚举包含所有的情况，因此直接计算即可。

求src1到\(i\)的距离可以使用Dijkstra算法，求\(i\)到dest的距离可以通过将边反向，求dest到各个点的距离来实现。

关于Dijkstra算法，本题如果不使用堆优化，会产生超时，因此顺带可以熟悉STL的使用。

STL使用 priority_queue 作为堆，默认是大根堆，因此为了得到最短路，可以将路径取相反数，放进大根堆。同时在Dijkstra算法中，用堆优化的时候，堆内的元素包含距离和顶点，因此使用 pair 记录距离和顶点。将 pair 放进 priority_queue 时，默认的排序方式是先排第一个，再排第二个。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
public:
#define MAXN 100000+20
typedef pair<long long, int> pp;
vector<vector<int>> v1, v2, w1, w2;
long long dis1[MAXN], dis2[MAXN], dis3[MAXN], now = -1;
    
    void getDis(int o, int n, long long *dis, int *vis, vector<vector<int>>& v, vector<vector<int>>& w)  {
        for (int i = 0; i < n; i++)  dis[i] = -1;
        priority_queue<pp> q;
        q.push(pp(0, o));
        while (!q.empty())  {
	        pp p = q.top();  q.pop();
	        int sn = p.second;
	        long long val = -p.first;
	        if (dis[sn] >= 0)  continue;
	        dis[sn] = val;
	        for (int i = 0; i < v[sn].size(); i++)
	            q.push(pp(-val - w[sn][i], v[sn][i]));
        }
    }

    long long minimumWeight(int n, vector<vector<int>>& edges, int src1, int src2, int dest) {
        int vis[MAXN];
        v1 = v2 = w1 = w2 = vector<vector<int>>(n);

        for (auto &edge : edges)  {
            v1[edge[0]].push_back(edge[1]); w1[edge[0]].push_back(edge[2]);
            v2[edge[1]].push_back(edge[0]); w2[edge[1]].push_back(edge[2]);	    
        }

        getDis(src1, n, dis1, vis, v1, w1);
        getDis(src2, n, dis2, vis, v1, w1);
        getDis(dest, n, dis3, vis, v2, w2);

        for (int i = 0; i < n; i++)  {
            if (dis1[i] == -1 || dis2[i] == -1 || dis3[i] == -1)  continue;
            if (now == -1)   now = dis1[i] + dis2[i] + dis3[i];
            if (dis1[i] + dis2[i] + dis3[i] < now)   
                now = dis1[i] + dis2[i] + dis3[i];
        }
        return now;
    }
};