Games202-Lecture3-4（Real-Time Shadows）学习笔记

发表于 更新于 分类于 本文字数： 1.3k 阅读时长 ≈ 1 分钟

本章内容

本章将讲述Real-Time Shadows（实时阴影）。

Shadow Mapping

一个2趟的算法

  • 第一遍从光源所在地方渲染场景，记录从光源位置出发得到的场景中最浅深度，得到 Shadow Map
  • 从相机位置出发，使用第一遍得到的深度（Shadow Map），来判断现在相机看到的位置是否在阴影里

一个完全在图像空间中的算法

  • 优点：如果 Shadow Map 已经生成，可以作为场景的几何表示，只需要 Shadow Map即可
  • 缺点：会导致自遮挡和走样（锯齿）

流程

详见 Games101-Lecture7-9（Shading）学习笔记

自遮挡

image-20220826145951697

如图所示，地板上存在一圈一圈的纹路，这是由于数值精度造成的结果。

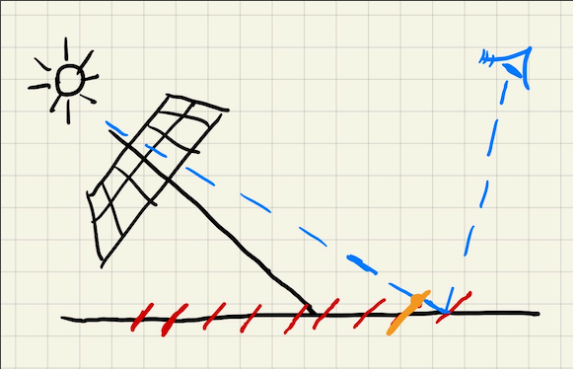
image-20220826151459399

如图所示，从左上角光源看向场景，我们沿着某个像素看过去时，我们会认为在这个像素对应的场景区域内都是某个深度值，也就是图中的地板上的红线。
而后，对于最右边红线上的点，当相机指向它，我们将该点与光源连线，发现光源上记录该点的深度是连线上与橙线的交点，所以光源与相机记录的深度存在细微的区别，shadow map 上记录的更浅，同时 shadow map 记录的深度是不连续的。
光源的角度比较偏的时候，造成的自遮挡现象会越为明显。

解决方法

  • 添加一个可变的 bias 作为精度参数，如上图所示，可以将橙线和红线的距离作为 bias 值，当光源和相机观测同一点的距离相距为 bias 时，认为它们是同一位置。效果如下图所示。

image-20220826204202343

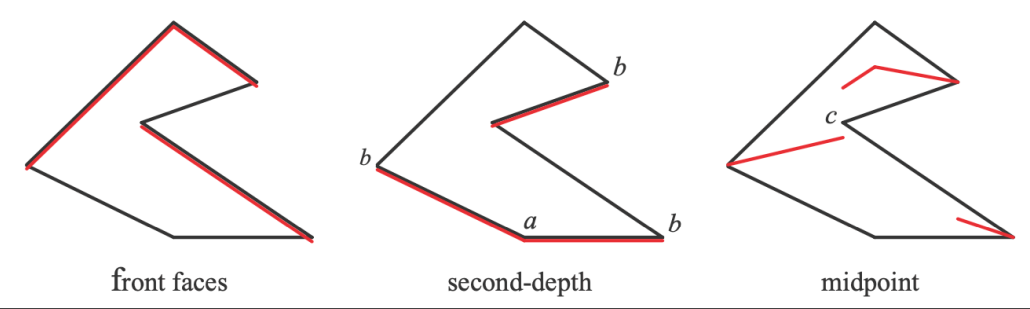
  • 存最小深度和次小深度，使用中间深度作为阴影比较。实际上很少使用这种方法。

image-20220826204540454

RTR 中的重要近似

\[ \int_\Omega f(x)g(x)dx \approx \frac{\int_\Omega f(x)dx}{\int_\Omega dx} * \int_\Omega g(x)dx \]

满足近似的 2 个条件：

  • g(x) 的支撑集足够小（支撑集可以简单地理解为积分域上积分不为0的部分）
  • g(x) 足够光滑

应用

image-20220827162241932

  • 对于点光源和方向光源，可以这样近似
  • 漫反射和恒定辐射光照

Percentage Closer Filtering（PCF）

用于阴影边界的抗锯齿

实现

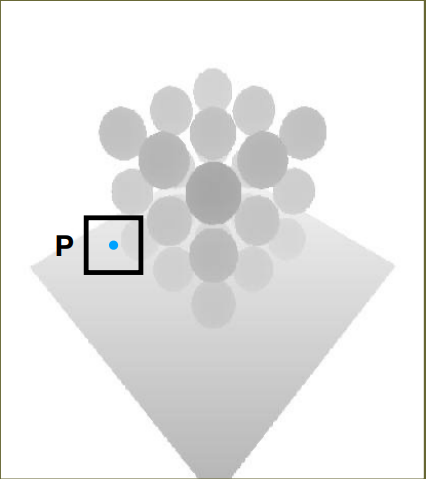
image-20220827164913817

  • 对每个像素点（如3 * 3）进行多次深度比较，如上图所示，对于p点，我们查询 shadow map 上该点周围3 * 3 的像素深度比较结果的平均。
  • 获得平均结果，1 表示无遮挡，0 表示遮挡，如
    1, 0, 1,
    1, 0, 1,
    1, 1, 0,
  • 获得是否遮挡的结果的平均，0.667（visibility）

关键结论

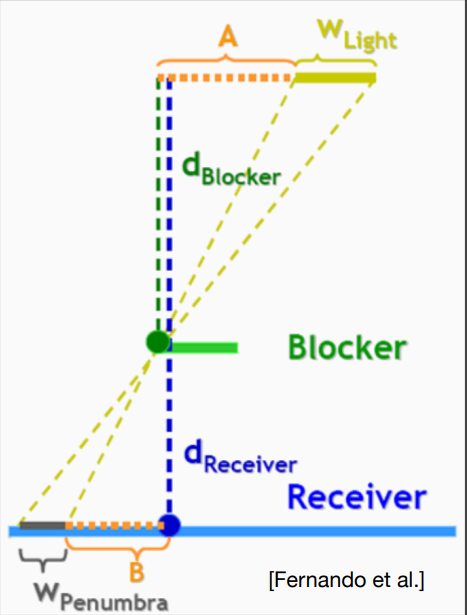image-20220827170236921 \[ w_{Penumbra} = (d_{Receiver} - d_{Blocker}) * w_{Light}/d_{Blocker} \] 如上图所示，w 区域表示阴影软硬的程度，w 越大，阴影越软。由相似三角形可知，当 Blocker 离 Light 越近的时候，w 则会越大，阴影越软。

Percentage Closer Soft Shadows

类似上文的 PCF 做法，用于产生软阴影，核心是适应性的 filter size

  • Blocker Search
    获得 Blocker 区域内的平均深度
  • Penumbra estimation
    使用 Blocker 区域内的平均深度来计算 filter 大小
  • 按 PCF 来计算

image-20220827171815441